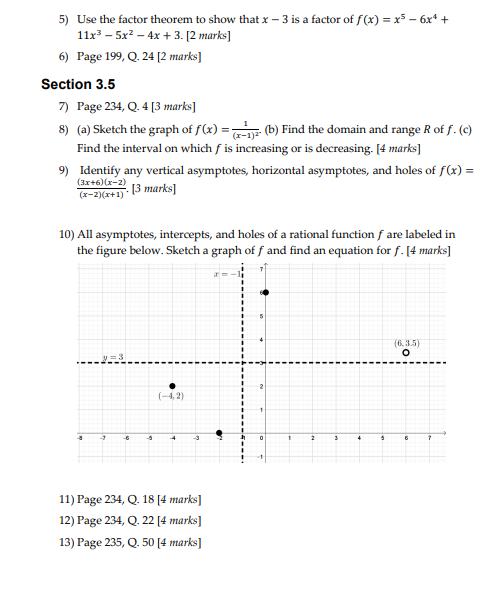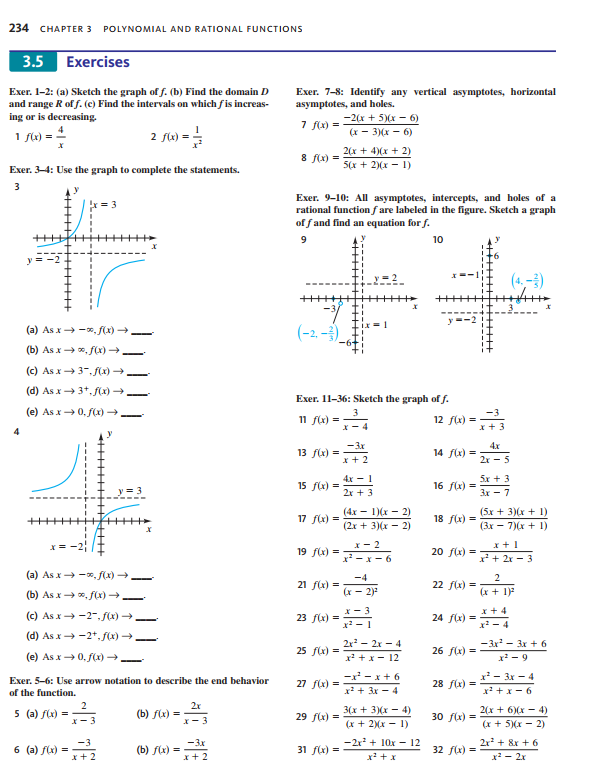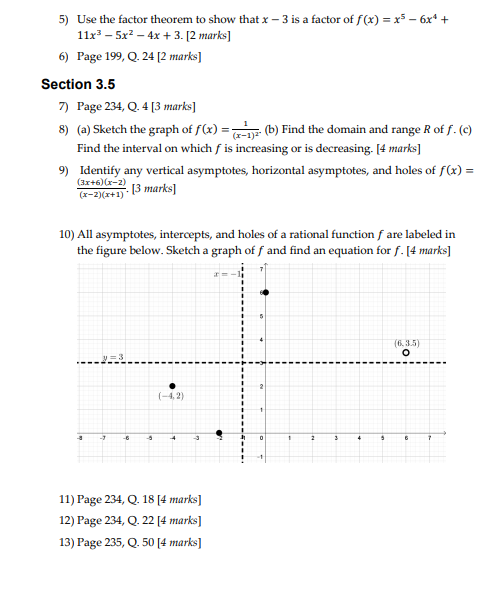
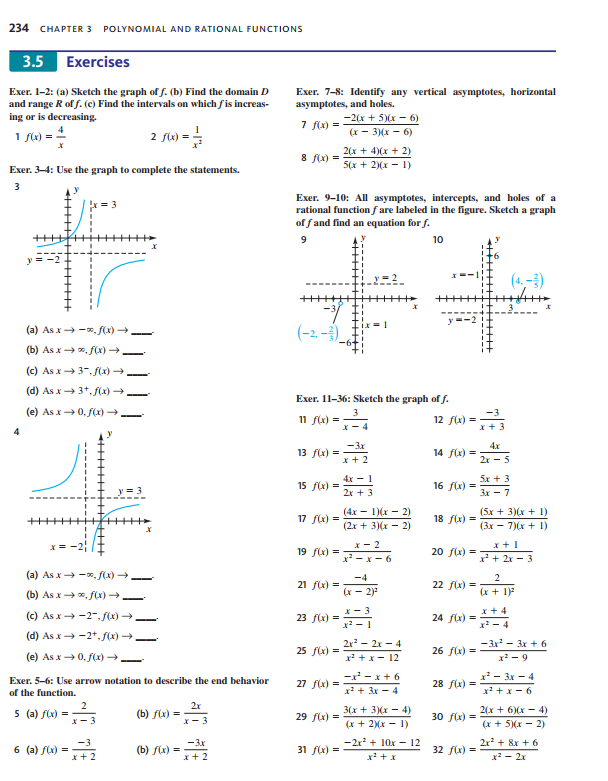


5) Use the factor theorem to show that x - 3 is a factor of / (x) = x5 - 6x* + 11x3 - 5x2 - 4x + 3. [2 marks] 6) Page 199, Q. 24 [2 marks] Section 3.5 7) Page 234, Q. 4 [3 marks] 8) (a) Sketch the graph of f(x) = 7_TE (b) Find the domain and range R of f. (c) Find the interval on which f is increasing or is decreasing. [4 marks] 9) Identify any vertical asymptotes, horizontal asymptotes, and holes of f(x) = (3r+6) (x-2) (x-2](r+1) . [5 marks] 10) All asymptotes, intercepts, and holes of a rational function f are labeled in the figure below. Sketch a graph of f and find an equation for f. [4 marks] (6. 3.5) O 2 (-4,2) 11) Page 234, Q. 18 [4 marks] 12) Page 234, Q. 22 [4 marks] 13) Page 235, Q. 50 [4 marks]234 CHAPTER 3 POLYNOMIAL AND RATIONAL FUNCTIONS 3.5 Exercises Exer. 1-2: (a) Sketch the graph of f. (b) Find the domain D Exer. 7-8: Identify any vertical asymptotes, horizontal and range R of f. (c) Find the intervals on which fis increase asymptotes, and holes. ing or is decreasing. 7 f(x) = - -2(x + 5)(x - 6) 1 f(x) = 4 2 f(x) = = (x - 3)(x - 6) 8 /(x) = = 2(x + 4)(x + 2) Exer. 3-4: Use the graph to complete the statements. "5(x + )(x - 1) 3 = 3 Exer. 9-10: All asymptotes, intercepts, and holes of a rational function fare labeled in the figure. Sketch a graph of f and find an equation for f. 9 10 -7 (4. - 2) (a) Asx - -x, f(x) (-2, -3) (b) As x - *, f() - (c) As x - 3-,/(x) = (d) As x - 3+, f(x) = Exer. 11-36: Sketch the graph of f. (e) As x - 0,/() = _ 11 /(x) = x - 4 12 /(x) = -3 * + 3 13 f(x) = - -Ar A.x x + 2 14 /(x) = = 2r - 5 = 3 15 f(x) = Ax - 1 2x + 3 16 /C) = 5.x + 3 Ar - 7 17 f(x) = (4x - 1)(x - 2) 18 /(x) = (5x + 3)(x + 1) (2r + 3)(x - 2) (3x - 7) (x + 1) * = x-2 19 /(x) = 1 - x - 6 20 (x) = 1+ 2x - 3 (a) As x - -*, f(x) 21 /(x) = -4 22 (x) = 2 (b) As x - x, /() _ (x - 2)3 (x + 1) (c) As x - -2-, f(x) - 23 /(x) = 12 - 1 24 /(x) =_ I - 4 (d) As x - -2+, f(x) - 25 /(x) = : 2x3 - 2r - 4 -3r - Ir + 6 (e) As x - 0,/() __ x' t x - 12 26 /(x) = - 1 - 9 Exer. 5-6: Use arrow notation to describe the end behavior 27 /(x) = - -F-x+6 28 Mixed - 3x - 4 of the function. x3 + 3x -4 x3+x-6 5 (a) f(x) = 2r x - 3 (b) fix) = Y - 3 29 /() = 24 3(x + 3)(x - 4) 30 fix) = 4(x + 6)(x - 4) (x + 2)(x - 1) (r + 5)(x - 2) 6 (a) f(x) = (b) fix) = -3x 31 /(x) = _2r + 10x - 12 2 + & + 6 x + 2 x + 2 32 /(x) = x3 - 2x3.2 Properties of Division 199 The easiest way to find the remainder using a graphing utility is to simply find the function value Y, when x = -1.37. However, the purpose of this example was to point out the graphical relationship to the division process. 3.2 Exercises Exer. 1-8: Find the quotient and remainder iff(x) is divided 22 degree 3; zeros -3, 0, 4 by p(x). 1 f(x) = 2x* - x' - 3x' + 7x - 12; p(x) = x] - 3 23 degree 4: zeros -2,$1, 4 24 degree 4; zeros -3, 0, 1, 5 2 f(x) = 3r*+ 2x-x-x-6; p(x) =x+ 1 3 /(x) = 3r' + 2x - 4; p(x) = 283 + 1 Exer. 25-32: Use synthetic division to find the quotient and remainder if the first polynomial is divided by the second. 4 f(x) = 1 - 5p - 4x - 8; p(x) = 2x3 + x 25 2r' - 3x3 + 4x - 5; x - 2 5 /(x) = 7x + 2; p(x) = 2x - x - 4 26 Ar' + 10x3 - 7x + 8 x + 4 6 f(x) = -5x3 + 3; p(x) = x- 3x+ 9 27 x - &r - 5; r+3 28 5x - 18x3 - 15; 7 /(x) = 10x + 4; p(x) = 2x - 5 29 Ar' + 6r' + 7; 8 f(x) = 70'+ 3x - 10; p(x)=x - x+ 10 30 -2x* + 10x - 3; x - 3 Exer. 9-12: Use the remainder theorem to find fle). 31 4r - 5r' + 1; 9 f(x) = 3-x -4; c = 2 32 9r' - 6r' + 3x - 4; x- 10 f(x) = 2r' + 4x' - 3x - 1; c = 3 11 f(x) = x - 6r' + 4x - 8; c= -3 Exer. 33-40: Use synthetic division to find fic). 12 fix) = x4 + 3 - 12; c= -2 33 /(x) = 2r' + 3x - Ar + 4; c= 3 Exer. 13-18: Use the factor theorem to show that r - c is a 34 /(x) = -x+ 4x+ x C= -2 factor of f(x). 35 /(x) = 0.3x3 + 0.4r; c=-0.2 13 /(x) = x + x - 2r + 12; c= -3 36 /(x) = 0. Lr' + 0.5x C = 0.3 14 /x) =r ty' - Ilx+ 10; c = 2 37 /(x) = 27r + 2p' + 1 c= : 15 /(x) = 1" - 4096; c= -2 38 /(x) = &r' - 3x3 + 7; 16 /(x) = > + 1024; C= -4 39 /(x) = x' + 3 - 5; c = 2+ V3 17 f(x) = x - 2p' + 3x - 36; c= ] 18 fix) = x - 3 + 5x - 2, c= 2 40 fix) = x - 1 - 8; c= 1+ v2 Exer. 19-24: Find a polynomial f(x) with leading coefficient Exer. 41-44: Use synthetic division to show that e is a zero I and having the given degree and zeros. of fur). 19 degree 3; zeros -2, 0, 5 41 (x) = 3 + & - 2p3 - 10r + 4; c= -2 20 degree 3; zeros 12, 3 42 f(x) = 4x3 - 9x3 - &x - 3; c = 3 21 degree 3; zeros 13, I 43 f(x) = 4' - 6r' + 8 - 3;3.5 Rational Functions 235 33 /x) = - 1 34 Arz * - 2x + 1 53 vertical asymptotes: I = -3, x = 1 *3 - Ax x - 9x horizontal asymptote: y = 0 X-intercept: -1; /(0) = -2 35 /x) = ir 36 Ari = - 4 hole at x = 2 x3 + 1 x3 + 1 54 vertical asymptotes: x = -1, x = 3 Exer. 37-40: Find the oblique asymptote, and sketch the horizontal asymptote: y = 2 graph of f. x-intercepts: -2, I; hole at r = ( 37 fix) 2 - x - 6 38 /(x) = = 2x1 - x - 3 65 A container for radioactive waste A cylindrical container for storing radioactive waste is to be constructed from lead. 39 fix) = 8 - x 40 /(x) = This container must be 6 inches thick. The volume of the outside cylinder shown in the figure is to be 167 fi'. Exer. 41-42: Find the curvilinear asymptote. (a) Express the height h of the inside cylinder as a function of the inside radius r. 41 fixed - x - 5 42 fixer - 3 - 2+ 1 x - 2 x - 3 (b) Show that the inside volume V(r) is given by Vr) = = 16 Exer. 43-50: Simplify fux), and sketch the graph of f. (r + 0.5) 43 fix) = 2 + x - 6 44 Ariz X- x - 6 (c) What values of r must be excluded in part (b)? x3 + 3x + 2 x3 - 2r - 3 EXERCISE 55 45 fixi z X - 1 46 /x) = * + 2 1 - x 73 - 4 47 fix =+ x - 2 x+ 2 48 Axis J - 2pl - 4x + 8 x - 2 49 fix = d' + 4x + 4 x3 + 3x + 2 56 Drug dosage Young's rule is a formula that is used to modify adult drug dosage levels for young children. If a (x3 + x)(2x - 1) denotes the adult dosage (in milligrams) and if r is the age 50 /(x) = = (x] - 3.x + 2)(2x - 1) of the child (in years), then the child's dose y is given by the equation y = fa/(r + 12). Sketch the graph of this equation for 1 > 0 and a = 100. Exer. 51-54: Find an equation of a rational function f that 57 Salt concentration Salt water of concentration 0.1 pound of salt per gallon flows into a large tank that initially con- satisfies the given conditions. ains 50 gallons of pure water. 51 vertical asymptote: x = 5 horizontal asymptote: y = -1 (a) If the flow rate of salt water into the tank is 5 gal/min, X-intercept: 2 find the volume Vr) of water and the amount A() of salt in the tank after r minutes. 52 vertical asymptotes: 1 = -2, 1 = 0 (b) Find a formula for the salt concentration c() (in lb/gal) horizontal asymptote: y = 0 after / minutes. *-intercept: 2; /(3) = 1 (c) Discuss the variation of c() as /