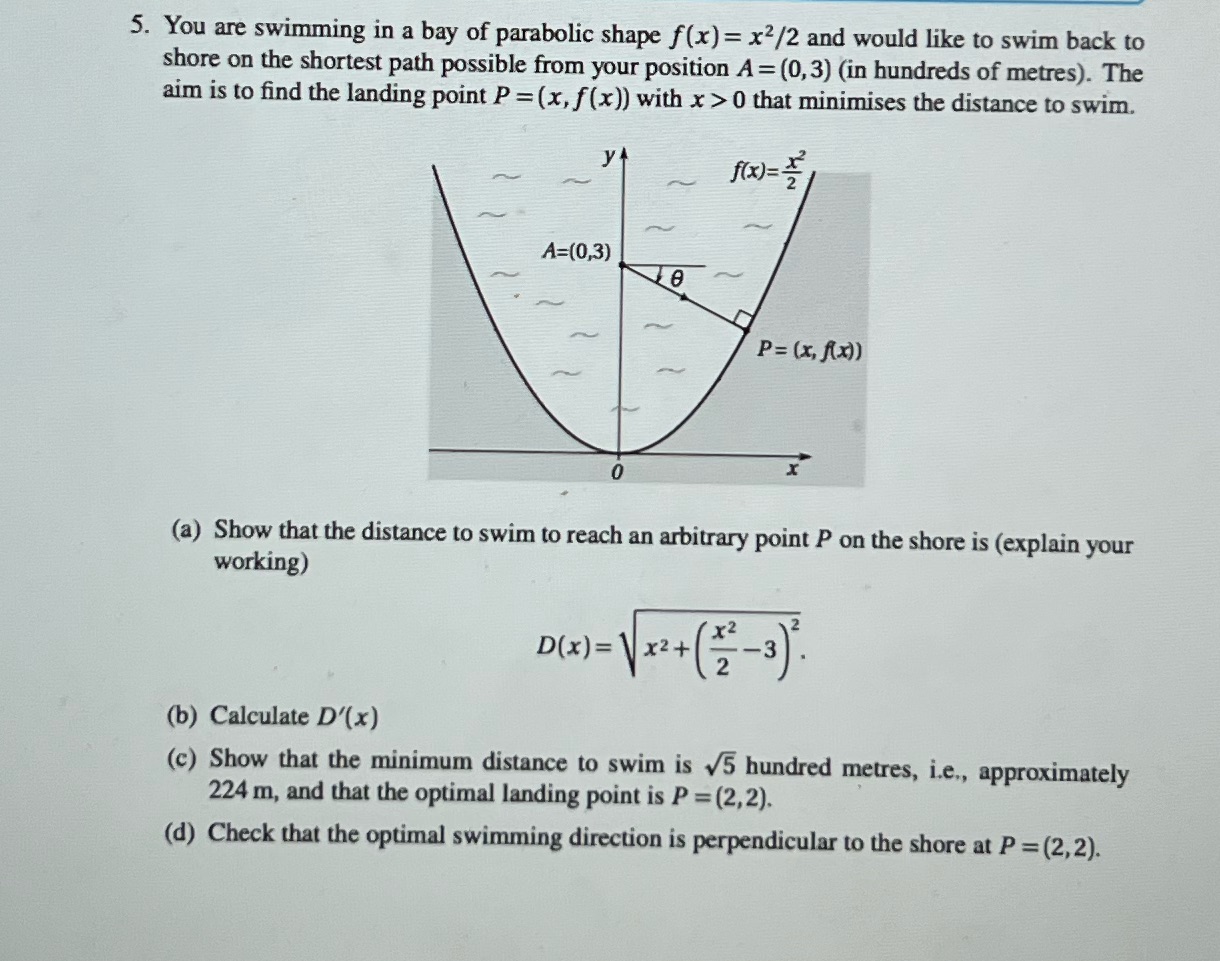
5. You are swimming in a bay of parabolic shape f(x) = x/2 and would like to swim back to shore on the shortest path possible from your position A=(0,3) (in hundreds of metres). The aim is to find the landing point P = (x, f(x)) with x>0 that minimises the distance to swim. y f(x)= A=(0,3) 8 P= (x, f(x)) 0 (a) Show that the distance to swim to reach an arbitrary point P on the shore is (explain your working) (b) Calculate D'(x) D(x)=x+ (c) Show that the minimum distance to swim is 5 hundred metres, i.e., approximately 224 m, and that the optimal landing point is P = (2,2). (d) Check that the optimal swimming direction is perpendicular to the shore at P=(2,2).