5.6 correct answers only

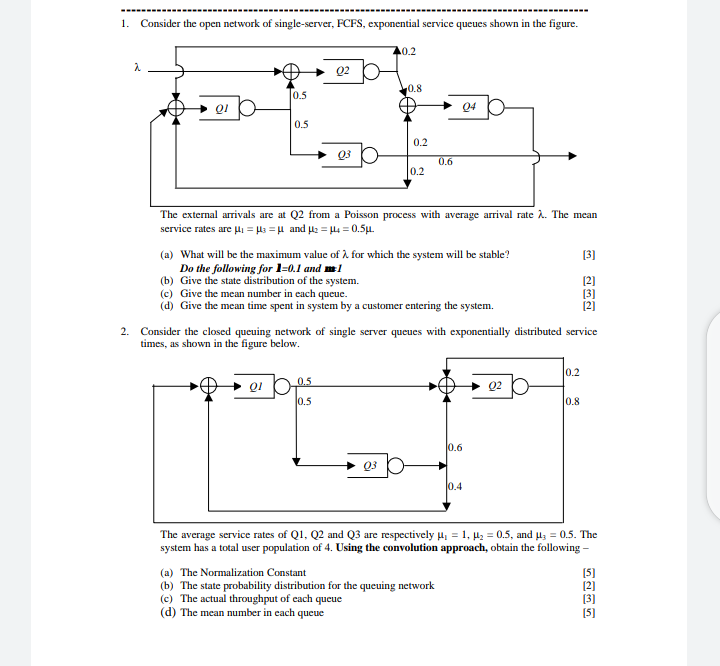
1. Students enter the mess for breakfast in equally likely groups of either one or two with a group arrival rate of 1. The first member of the group is served in an exponentially distributed time X with pdf b(t) and LST B(s). The second member (if any) orders an extra omelet which requires D seconds more where D is fixed. The mess operates as a Single-Server M("/G/1 queue. Find the mean delay that an arriving student will encounter before being served. [10) 2. Consider a 2-priority preemptive resume priority M/G/1 queue with high priority customers of Class 2 and lower priority customers of Class 1. The system enforces the rule that there can be only one Class 2 customer in the system at any time (i.e. there is no buffering for Class 2) - however, there is infinite buffering for Class 1 customers. Let X2 (FIXED) be the service time for Class 2 and X, (FIXED) be the service time for Class 1. Arrival processes are Poisson with average arrival rate I, for Class 1 and 12 for Class 2. For this, consider a Class 1 customer who start service at time f and leaves the system at time f+7. What would be the distribution (or L.S.T.) of the random variable 7? [Hint: You can assume a Poisson distribution at the appropriate place without explicitly deriving it.] [10] 3. Consider the system of Problem 2 once again except that we now assume that Class 2 customers can also be infinitely buffered. For this obtain the average total delays encountered by Class 2 and Class 1 customers.1. Consider the open network of single-server, FCPS, exponential service queues shown in the figure. 40.2 05 04 03 0.6 0.2 The external arrivals are at Q2 from a Poisson process with average arrival rate 2. The mean service rates are li = : = [ and He = 14 = 0.5p. (a) What will be the maximum value of A for which the system will be stable? [3] Do the following for 1=0.1 and mal (b) Give the state distribution of the system. [2] (c) Give the mean number in each queue. (3] 'd) Give the mean time spent in system by a customer entering the system. 2. Consider the closed queuing network of single server queues with exponentially distributed service times, as shown in the figure below. 1.2 0.5 02 05 0.8 0.6 03 10.4 The average service rates of Q1, Q2 and Q3 are respectively , = 1, My = 0.5, and Us = 0.5. The system has a total user population of 4. Using the convolution approach, obtain the following - (a) The Normalization Constant b) The state probability distribution for the queuing network [2] c) The actual throughput of each queue [3] (d) The mean number in each queue [5]1. Consider the open network of single-server, FCPS, exponential service queues shown in the figure. 40.2 0Z 0.5 014 0.2 0.6 07 The external arrivals are at Q2 from a Poisson process with average arrival rate 2. The mean service rates are 1 = = = [ and Je = 14 = 0.5j. (a) What will be the maximum value of A for which the system will be stable? (3] Do the following for 1=0.1 and ml (b) Give the state distribution of the system. [2] (c) Give the mean number in each queue. [3] (d) Give the mean time spent in system by a customer entering the system. (21 2. Consider the closed queuing network of single server queues with exponentially distributed service times, as shown in the figure below. 0.2 0.5 02 0.8 0.6 03 0.4 The average service rates of Q1, Q2 and Q3 are respectively , = 1, , = 0.5, and ; = 0.5. The system has a total user population of 4. Using the convolution approach, obtain the following - (a) The Normalization Constant [5] b) The state probability distribution for the queuing network [2] (c) The actual throughput of each queue (3] (d) The mean number in each queue [5]