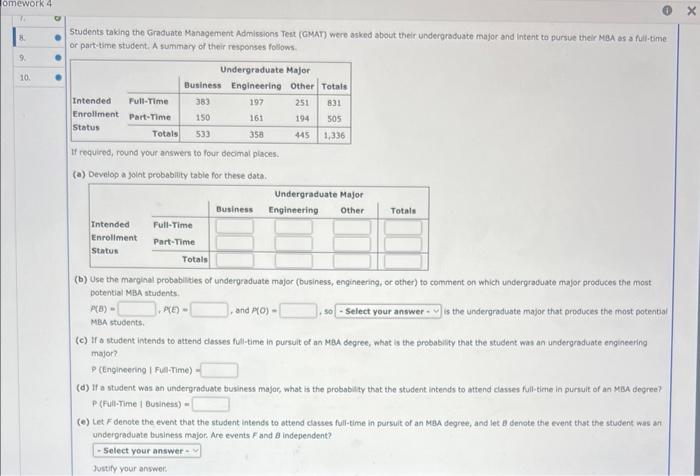
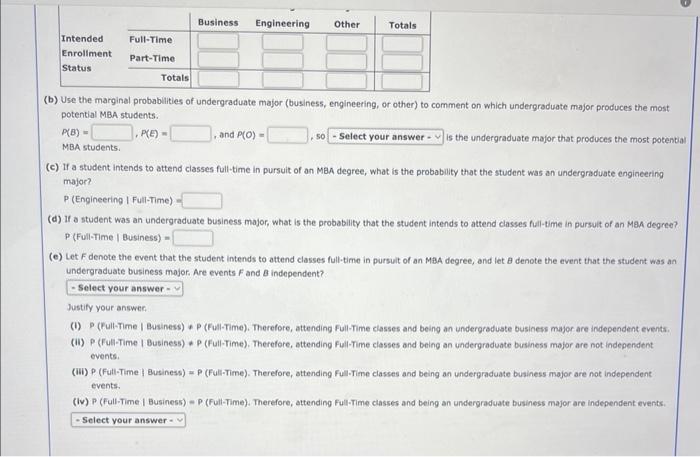
5tudents taking the Graduate Management. Admissions Test (GMAJ] were asked about their undergrodeate major and intent to pursue their Mat es a fullime or part-time student. A summary of their responses follows. If required, round your ansmers to four decimat piaces. (a) Develop a joint probability table for these data. (b) Use the marginal probabilities of undergraduate major (business, engineering, or other) to comment on which undergraduate major produces the most Dotential MBA students. P(B)=,andP(D)=,so=istheundergraduatemajorthatproducestheinostpotentialMBAstudents. (c) If a student intends to attend clesses full-time in pursuit of an MeA degree, what is the probability that the student was an undergraduate engineering major? P (Engineering | Fuatime) = (d) If a student was an undergraduate business major, what is the probabily that the student intends to attend classes full-time in pursuit of an Yad degree? P (Full-Time 1 Business) = (e) Let F denote the event that the student intends to attend classes full-time in pursuit of an MaA degree, and let a denote the event that the student was an andergraduate business major. Are events F and B independent? (b) Use the marginal probabilities of undergraduate major (business, engineering, or other) to comment on which undergraduate major produces the most potential MBA students. is the undergraduate major that produces the most potentia (c) If a student intends to attend classes full-time in pursuit of an MBA degree, what is the probability that the student was an undergraduate engineering major? P (Engineering I Full-Time) (d) If a student was an undergraduate business major, what is the probability that the student intends to attend classes full-time in pursuit of an MaA degree? P( Full-7ime | Business )= (e) Let F denote the event that the student intends to attend classes full-time in pursuit of an MaA degree, and let denote the event that the student was an undergraduate business major. Are events F and B independent? Justify your answec. (i) P (Full-Time I Business) \& P (Full-Time). Therefore, attending Full-Time classes and being an undergraduste business major are independent events. (ii) P (Fuli-Time I Business) \& P (Full-Time). Therefore, attending Full-Time classes and being an undergraduate business major are not independent events. (iii) P (Futi-Time | Business) = P (Full-Time). Therefore, attending Ful-Time classes and being an undergraduate business major are not indopendent events. (iv) P (Full-Time I Business) = P. (Full-Time). Therefore, attending Full-Time classes and being an undergraduate business major are independent events