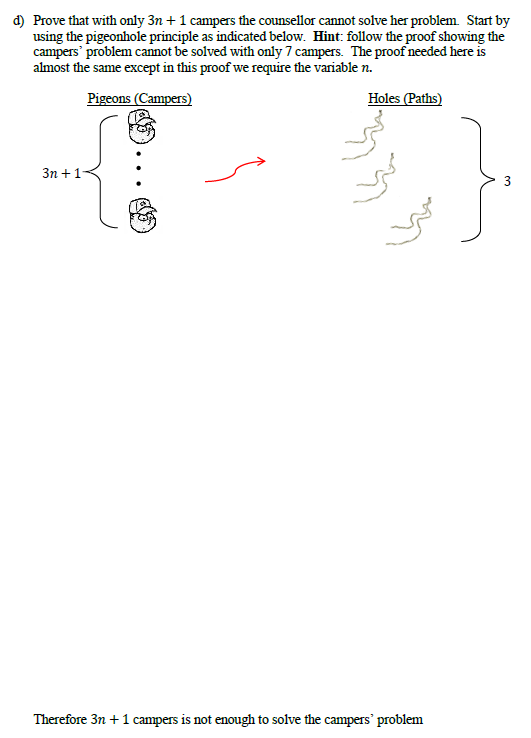
6. A counselor has 3n+2 campers with her at a junction in a hiking trail. She knows their camp is twenty minutes down one of four possible paths. It will be dark in one hour and the group must find their camp before dark n of the 3n+2 campers sometimes lie, and unfortunately the counselor doesn't know which n they are. She checks path 4, leaving paths 1, 2, and 3 for the 3n+2 campers. She sends n + 1 campers down each of paths 1 and 2 and sends n campers down path #3. Then she designs a code containing three codewords to deduce the location of the camp if she doesn't find it down path 4. Each codeword will represent the camp being down a particular path. Each bit (1 or 0) in the codeword will represent the answer given by a camper, a 1 will represent "yes" and a 0 will represent "no". Here is the counselor's code: Codeword #1: Codeword #2: Codeword #3: The camp is down path 1 and no one lies: 11 ... 11 00...0000... 0 The camp is down path 2 and no one lies: 00...00 11 ... 11 00...0 The camp is down path 3 and no one lies: 00... 00 00...00 11... 1 Responses from the n +1 campers sent down path #1 Responses from the n +1 campers sent down path #2 Responses from the n campers sent down path #3 a) Find the minimum hamming distance of the counselor's code. min H(x, y) = b) Is the hamming distance large enough to correct n corrupted bits and therefore deduce the location of the camp? (Circle one) Yes No c) The counselor has an even number of campers (so n is even) with her and needs to figure out if the camp is down path 1, 2, or 3. When she gets back to the junction she asks everyone what was found down their path. First asking everyone that went down path 1, then path 2, and finally path 3. The responses were recorded with bits and listed in order: 101010 --- 101 010101 ...010000000 ... 00 Where is the camp? The camp is down path: (Circle one of the four options) 1 2 3 this scenario will never occur d) Prove that with only 3n+ 1 campers the counsellor cannot solve her problem. Start by using the pigeonhole principle as indicated below. Hint: follow the proof showing the campers' problem cannot be solved with only 7 campers. The proof needed here is almost the same except in this proof we require the variable n. Pigeons (Campers) Holes (Paths) 3n +1 Therefore 3n + 1 campers is not enough to solve the campers' problem 6. A counselor has 3n+2 campers with her at a junction in a hiking trail. She knows their camp is twenty minutes down one of four possible paths. It will be dark in one hour and the group must find their camp before dark n of the 3n+2 campers sometimes lie, and unfortunately the counselor doesn't know which n they are. She checks path 4, leaving paths 1, 2, and 3 for the 3n+2 campers. She sends n + 1 campers down each of paths 1 and 2 and sends n campers down path #3. Then she designs a code containing three codewords to deduce the location of the camp if she doesn't find it down path 4. Each codeword will represent the camp being down a particular path. Each bit (1 or 0) in the codeword will represent the answer given by a camper, a 1 will represent "yes" and a 0 will represent "no". Here is the counselor's code: Codeword #1: Codeword #2: Codeword #3: The camp is down path 1 and no one lies: 11 ... 11 00...0000... 0 The camp is down path 2 and no one lies: 00...00 11 ... 11 00...0 The camp is down path 3 and no one lies: 00... 00 00...00 11... 1 Responses from the n +1 campers sent down path #1 Responses from the n +1 campers sent down path #2 Responses from the n campers sent down path #3 a) Find the minimum hamming distance of the counselor's code. min H(x, y) = b) Is the hamming distance large enough to correct n corrupted bits and therefore deduce the location of the camp? (Circle one) Yes No c) The counselor has an even number of campers (so n is even) with her and needs to figure out if the camp is down path 1, 2, or 3. When she gets back to the junction she asks everyone what was found down their path. First asking everyone that went down path 1, then path 2, and finally path 3. The responses were recorded with bits and listed in order: 101010 --- 101 010101 ...010000000 ... 00 Where is the camp? The camp is down path: (Circle one of the four options) 1 2 3 this scenario will never occur d) Prove that with only 3n+ 1 campers the counsellor cannot solve her problem. Start by using the pigeonhole principle as indicated below. Hint: follow the proof showing the campers' problem cannot be solved with only 7 campers. The proof needed here is almost the same except in this proof we require the variable n. Pigeons (Campers) Holes (Paths) 3n +1 Therefore 3n + 1 campers is not enough to solve the campers