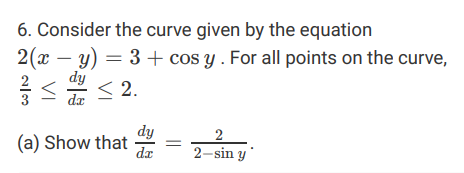
6. Consider the curve given by the equation 2(x - y) = 3 + cos y. For all points on the curve, dy < 2. da 2/3 (a) Show that = dy dr 2 2-sin y (b) For - (c) Determine the concavity of the curve at points for which - (d) Let y = f(x) be a function, defined implicitly by 2(x - y) = 3 + cos y, that is continuous on the closed interval [2, 2.1] and differentiable on the open interval (2, 2.1). Use the Mean Value Theorem on the interval [2, 2.1] to show that (2.1) (2) . 15