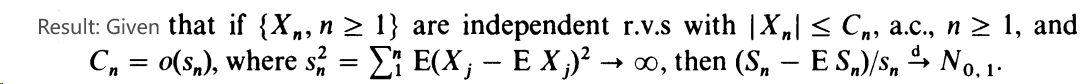
6. Let {X} be independent with P{Xn = 1} = P{X, = 0} 1 2a P{Xn = +n} = - = ( 1 ) ( 1 ), n 1, 4 ()() n 1, a > 1. 1 Again, Sn has a limiting normal distribution despite the Lindeberg condition being vitiated. Hint: You should find the Lindeberg condition doesn't hold. The next steps are using B-C lemma, Slutsky's theorem, the following result provided. You may want to divide Sn/sqrt(n) into 2 parts. Result: Given that if {X,, n 1} C = o(s), where s = are independent r.v.s with |X| , a.c., n 1, and E(X; - E X;) , then (S, ES)/Sn No. 1- -