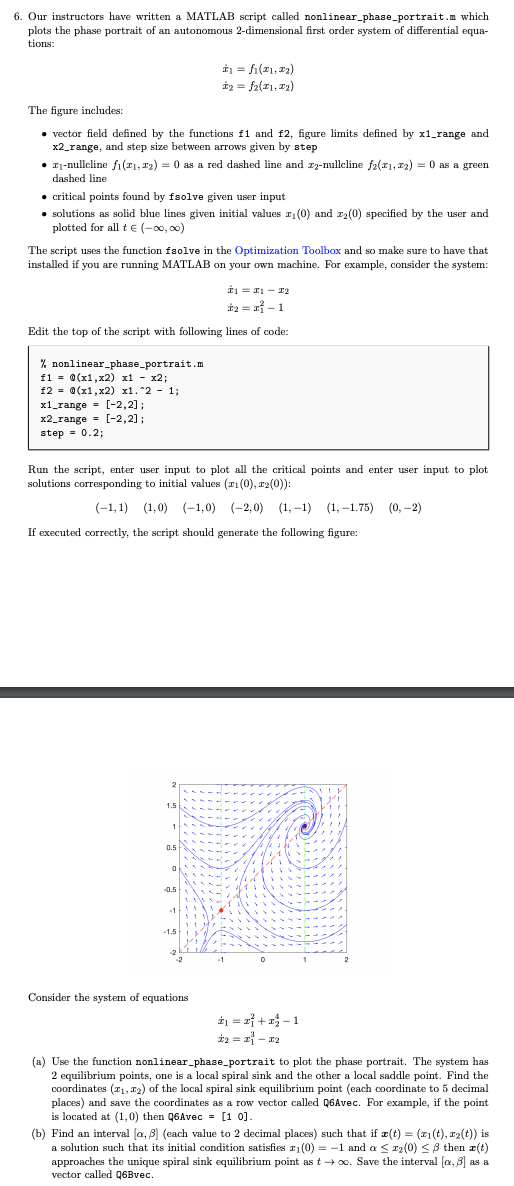
6. Our instructors have written a MATLAB script called nonlinear_phase_portrait.m which plots the phase portrait of an autonomous 2-dimensional first order system of differential equa- tions: The figure includes: vector field defined by the functions f1 and f2, figure limits defined by x1_range and x2_range, and step size between arrows given by step -nullcline f1 (11, 2) = 0 as a red dashed line and z2-nullcline f2(#1, #2) = 0 as a green dashed line critical points found by fsolve given user input solutions as solid blue lines given initial values (0) and 22 (0) specified by the user and plotted for all t (-00,00) The script uses the function faolve in the Optimization Toolbox and so make sure to have that installed if you are running MATLAB on your own machine. For example, consider the system: # = - 12 * = x-1 Edit the top of the script with following lines of code: % nonlinear_phase_portrait.m f1= @(x1,x2) x1 - x2; f2= @(x1, x2) x1.2 1; x1_range= [-2,2]; x2_range = [-2,2]; step = 0.2; Run the script, enter user input to plot all the critical points and enter user input to plot solutions corresponding to initial values (#(0), 12(0)): (-1,1) (1,0) (-1,0) (-2,0) (1,-1) (1,-1.75) (0, -2) If executed correctly, the script should generate the following figure: 2 1.5 1 0.5 # = f(#1, #) #2 = f2(#1, #2) 0 -0.5 -1 -1.5 Consider the system of equations = x+-1 2 = 1 - x2 (a) Use the function nonlinear_phase_portrait to plot the phase portrait. The system has 2 equilibrium points, one is a local spiral sink and the other a local saddle point. Find the coordinates (1, 12) of the local spiral sink equilibrium point (each coordinate to 5 decimal places) and save the coordinates as a row vector called Q6Avec. For example, if the point is located at (1,0) then Q6Avec = [10]. (b) Find an interval [a, 6] (each value to 2 decimal places) such that if (t) = (x(t), (t)) is a solution such that its initial condition satisfies z(0) = -1 and a z(0) then r(t) approaches the unique spiral sink equilibrium point as to. Save the interval [a, 8] as a vector called Q6Bvec.