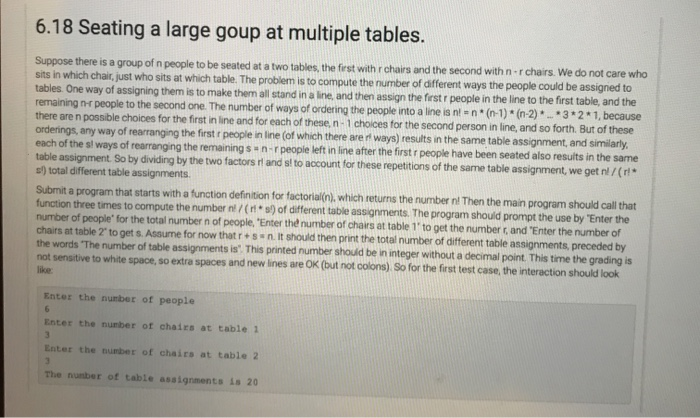
6.18 Seating a large goup at multiple tables. Suppose there is a group of people to be seated at a two tables, the first with r chairs and the second with nor chairs. We do not care who sits in which chair, just who sits at which table. The problem is to compute the number of different ways the people could be assigned to tables. One way of assigning them is to make them all stand in a line, and then assign the first people in the line to the first table, and the remaining nr people to the second one. The number of ways of ordering the people into a line is n = n(n-1)(n-2)*_*3*2*1, because there are n possible choices for the first in line and for each of these, n-1 choices for the second person in line, and so forth. But of these orderings, any way of rearranging the first people in line (of which there are ways) results in the same table assignment, and similarly, each of the st ways of rearranging the remaining sun-r people left in line after the first people have been seated also results in the same table assignment. So by dividing by the two factors and sito account for these repetitions of the same table assignment, we get nl /(r! s) total different table assignments. Submit a program that starts with a function definition for factorial(n), which returns the number n! Then the main program should call that function three times to compute the number n ( s) of different table assignments. The program should prompt the use by 'Enter the number of people for the total number n of people, "Enter the number of chairs at table 1' to get the number and 'Enter the number of Chairs at table to get s. Assume for now thatron. It should then print the total number of different table assignments, preceded by the words 'The number of table assignments is' This printed number should be in integer without a decimal point. This time the grading is not sensitive to white space, so extra spaces and new lines are OK (but not colons) So for the first test case, the interaction should look Enter the number of people Enter the number of chairs at table 1 Enter the number of chairs at table 2 The number of table assignments is 20