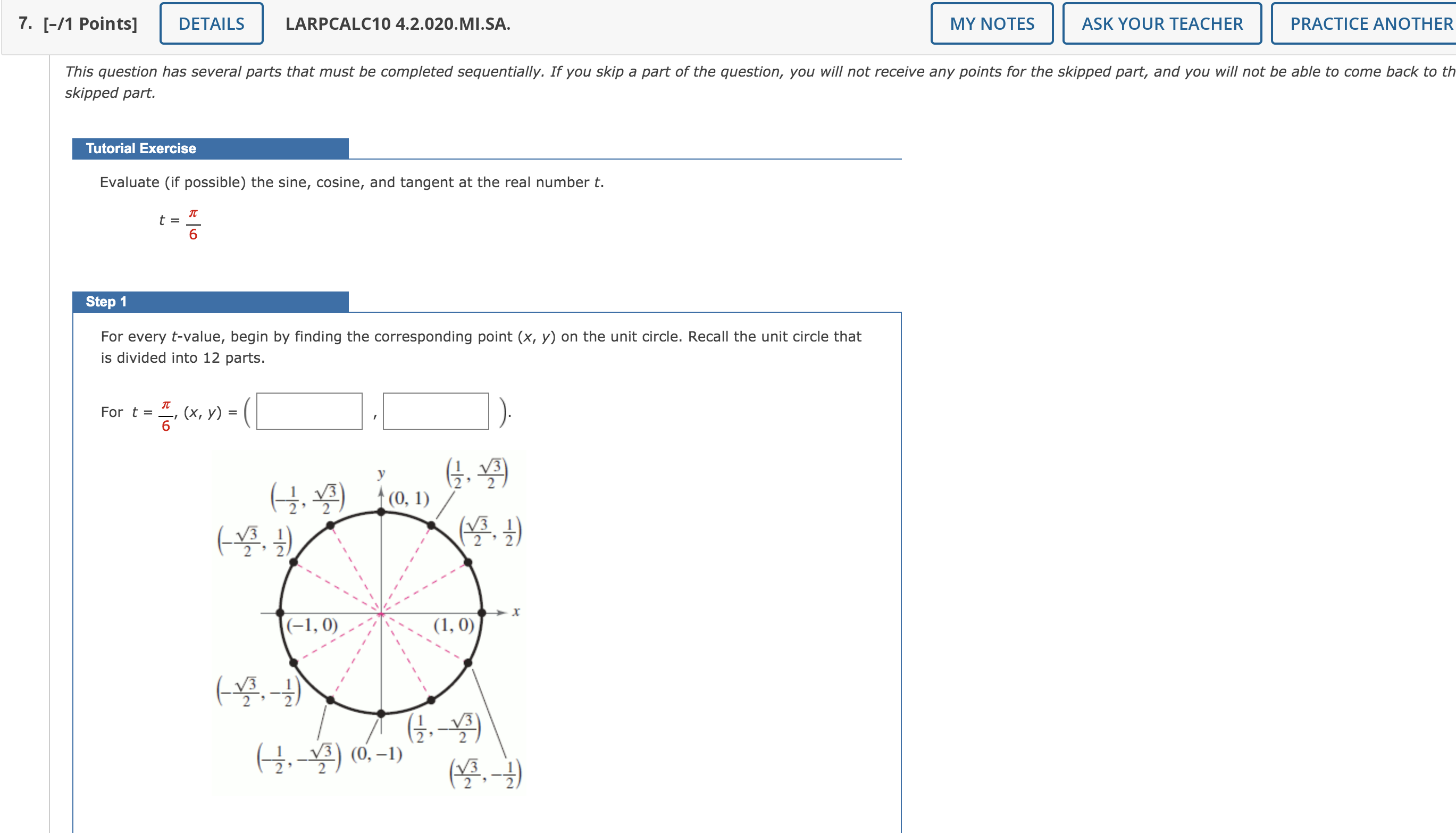
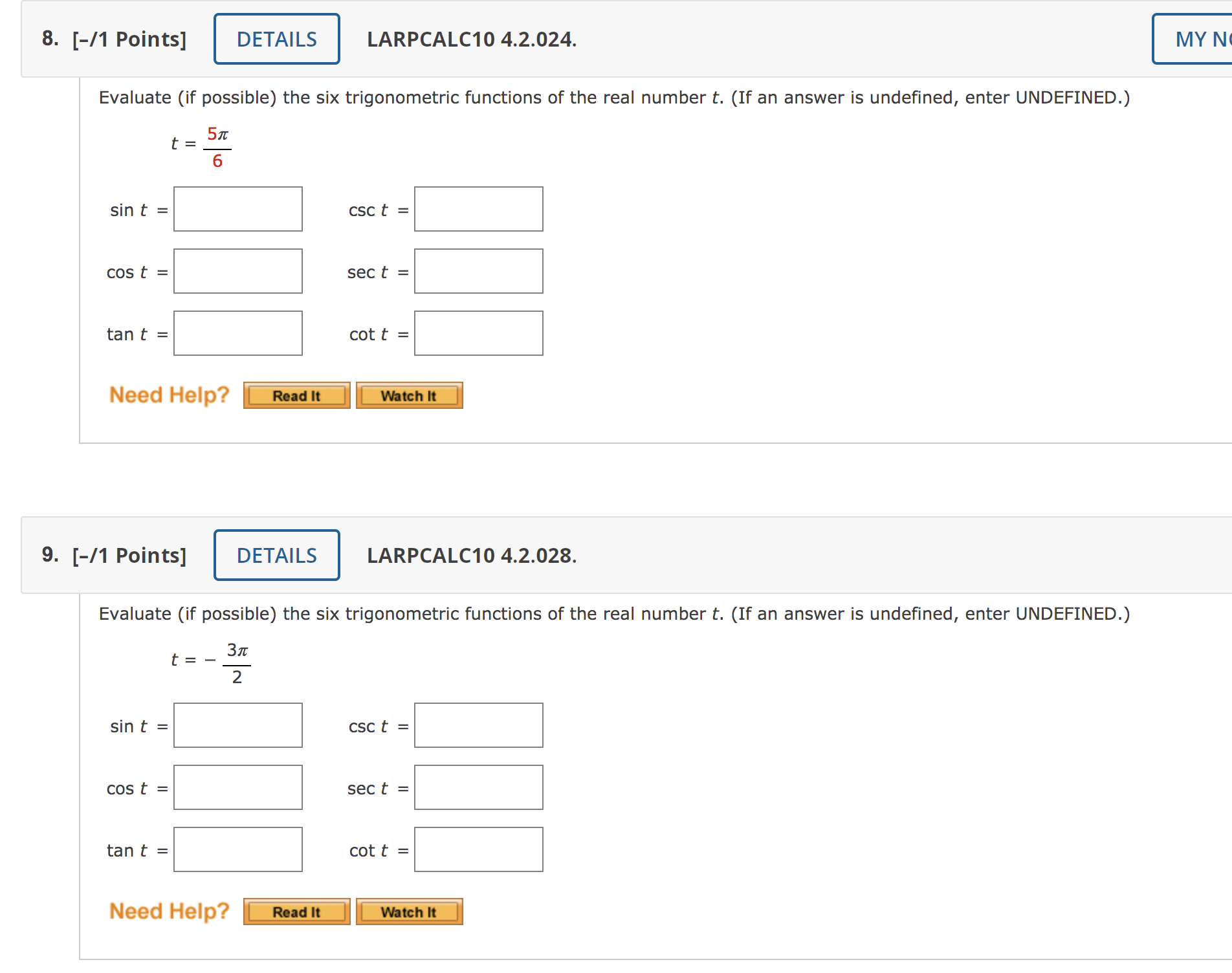
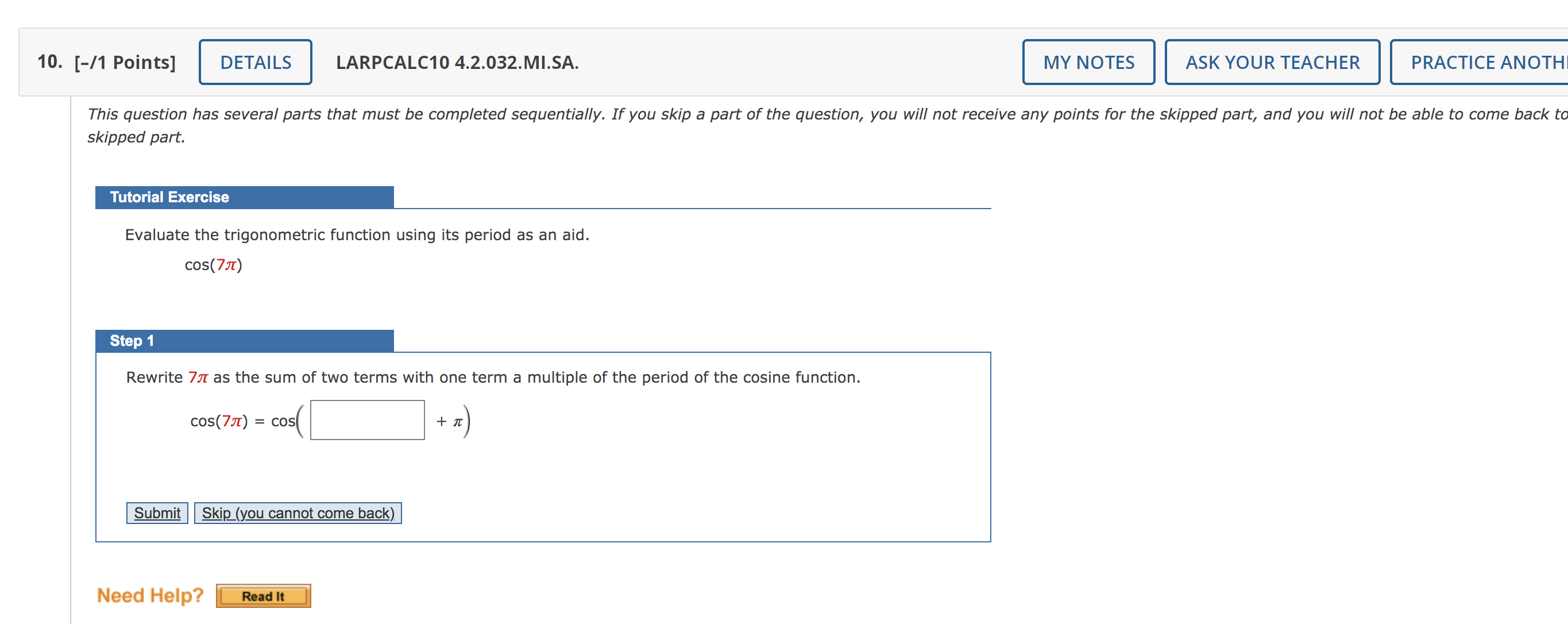
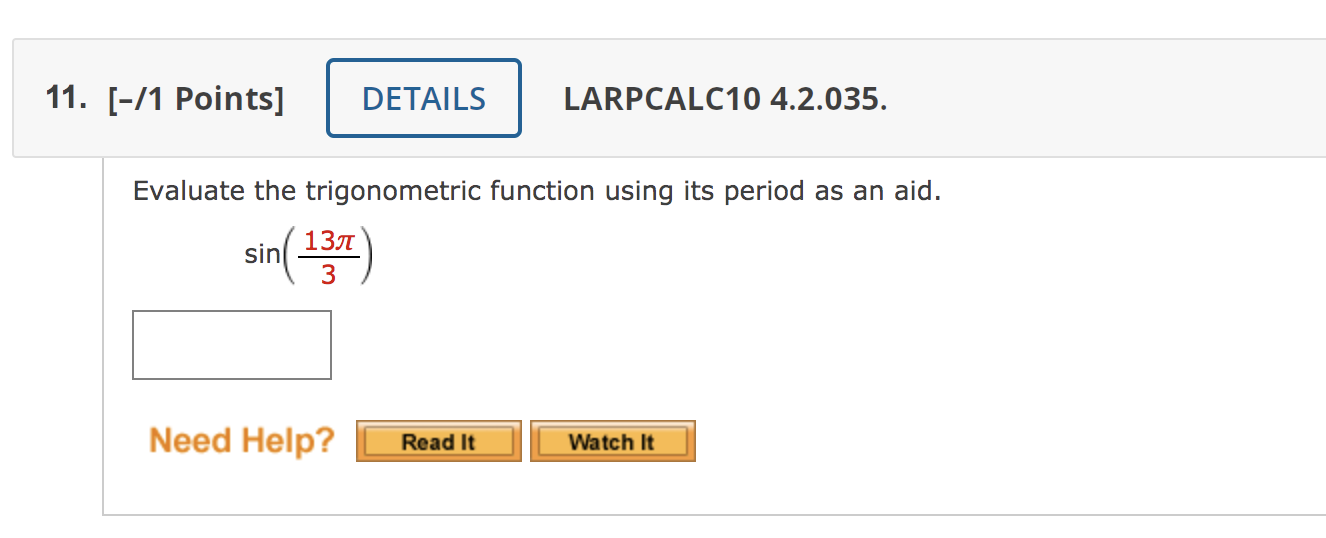
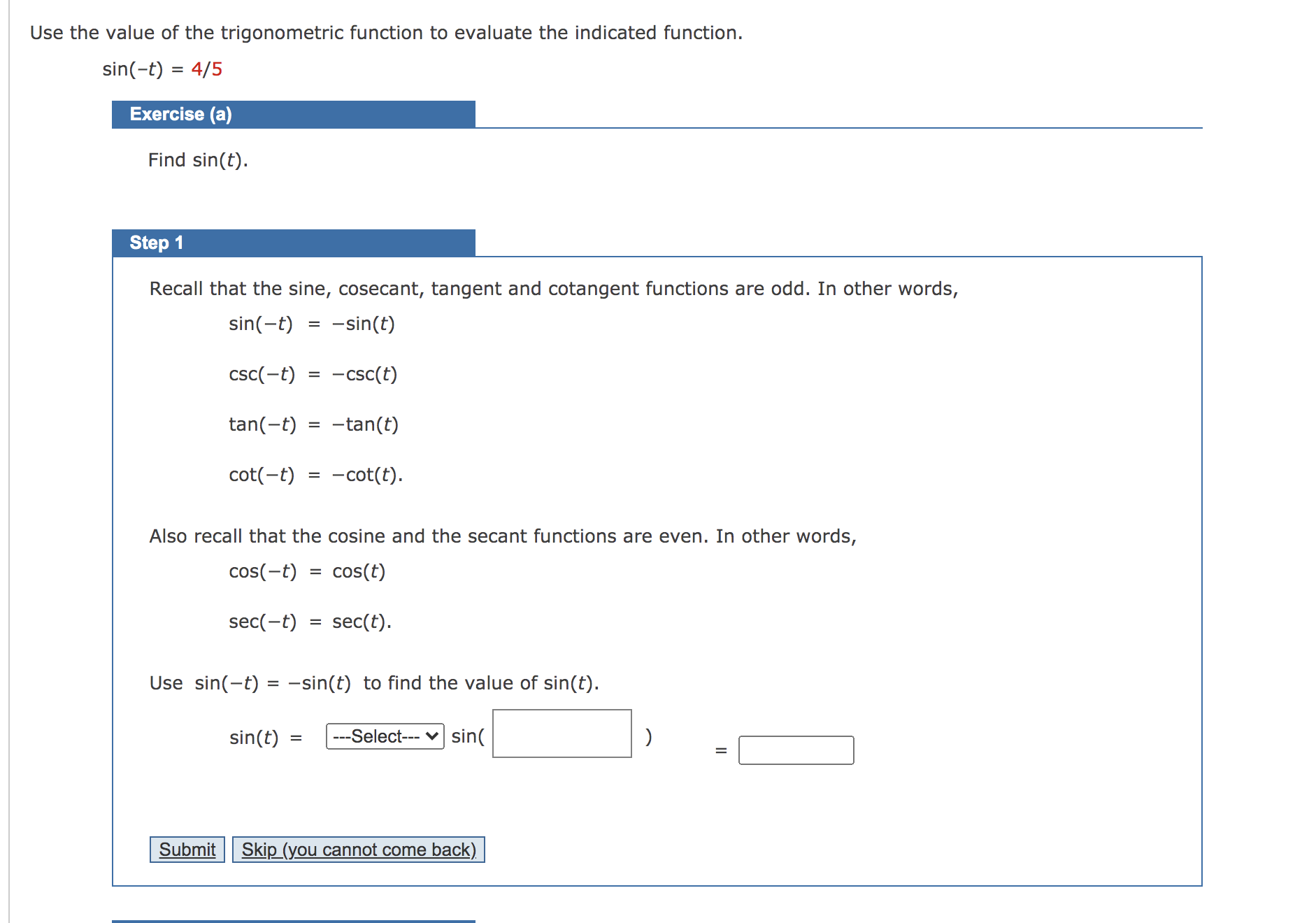
7. [-/1 Points] DETAILS LARPCALC104.2.020.MI.SA. skipped part. Tutorial Exercise t\" 6 is divided into 12 parts. Evaluate (if possible) the sine, cosine, and tangent at the real number t. For every t-value, begin by nding the corresponding point (x, y) on the unit circle. Recall the unit circle that For t=%,(x,y)=( y (a A?) (0.1)/ L'% X MY NOTES ASK YOUR TEACHER | PRACTICE ANOTHER This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to th 8. [-/1 Points] DETAILS LARPCALC10 4.2.024. MY N Evaluate (if possible) the six trigonometric functions of the real number t. (If an answer is undefined, enter UNDEFINED.) t = 6 sin t = csc t = cos t = sec t = tan t = cot t = Need Help? Read It Watch It 9. [-/1 Points] DETAILS LARPCALC10 4.2.028. Evaluate (if possible) the six trigonometric functions of the real number t. (If an answer is undefined, enter UNDEFINED.) t = - 2 sin t = csc t = cos t = sec t = tan t = cot t = Need Help? Read It Watch It. [-/1 Points] LARPCALC10 4.2.032.MI.SA. - ASK YOUR TEACHER PRACTICE ANOTHl This question has several parts that must be completed sequentially. If you skip a part of the question, you will not receive any points for the skipped part, and you will not be able to come back to skipped part. Tutorial Exercise Evaluate the trigonometric function using its period as an aid. cos(77r) Rewrite 77! as the sum of two terms with one term a multiple of the period of the cosine function. cos(7.7r) = cos( + 7:) Submit g (you cannot come back) I Need Help? 11. [-11 Points] DETAILS LARPCALC1O 4.2.035. Evaluate the trigonometric function using its period as an aid. sin(13) 3 Z Need Help? Use the value of the trigonometric function to evaluate the indicated function. sin(t) = 4/5 @ Find sin(t). Recall that the sine, cosecant, tangent and cotangent functions are odd. In other words, sin(t) = sin(t) csc(t) = csc(t) tan(t) = tan(t) cot(t) = cot(t). Also recall that the cosine and the secant functions are even. In other words, cos(t) = cos(t) sec(t) = sec(t). Use sin(t) = sin(t) to find the value of sin(t). Sin(t) = ---Se|ect--V Sin(|:| ) = I: Submit Skip (you cannot come back)