Answered step by step

Verified Expert Solution

Link Copied!

Question

1 Approved Answer

Posted on Apr 15, 2024

7. Let {E} be a monotone sequence of sets, that is, Ek C Ek+1 for k = 1, 2,... or Ek+1 C Ek for

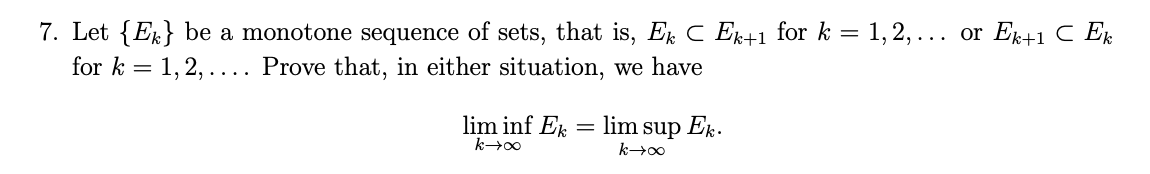
7. Let {E} be a monotone sequence of sets, that is, Ek C Ek+1 for k = 1, 2,... or Ek+1 C Ek for k = 1, 2,... Prove that, in either situation, we have lim inf Ek = lim sup Ek. 0043 k

Step by Step Solution

There are 3 Steps involved in it

Step: 1

Two scenarios will be examined for this proof 1 E k1 E k for every k For every k 1 E k E k1 Lets des... blur-text-image

Get Instant Access to Expert-Tailored Solutions

See step-by-step solutions with expert insights and AI powered tools for academic success

Step: 2

Step: 3

Ace Your Homework with AI

Get the answers you need in no time with our AI-driven, step-by-step assistance

Get Started

Recommended Textbook for

An Introduction to Analysis

Authors: William R. Wade

4th edition

132296381, 978-0132296380

More Books

Students also viewed these Mathematics questions

Question

Think about the machine metaphor, and the attributes of machines you read about. Discuss how you see people in both the operating room and the poultry plant as standardized, specialized, replaceable,...

Answered: 1 week ago

Question

QUIZ... Let D be a poset and let f : D D be a monotone function. (i) Give the definition of the least pre-fixed point, fix (f), of f. Show that fix (f) is a fixed point of f. [5 marks] (ii) Show that...

Answered: 1 week ago

Question

For monotone functions f, f0: P Q between posets (P, vP ) and (Q, vQ), let f v f(i) Prove that the binary relation v is a partial order. [3 marks] (ii) For monotone functions between posets p : P 0...

Answered: 1 week ago

Question

★★★★★

The atoms that constitute your body are mostly empty space, and structures such as the chair you're sitting on are composed of atoms that are also mostly empty space. So why don't you fall through...

Answered: 1 week ago

Question

★★★★★

A beam of wide-flange cross section (see figure) has the following dimensions: b = 120 mm, t = 10 mm, h = 300 mm, and h1 = 260 mm. The beam is simply supported with span length L = 3.0 m. A...

Answered: 1 week ago

Question

★★★★★

12-59. Household services such as cooking, cleaning, shopping, repairs, yard work, and management of household finances have economic value. a. True b. False

Answered: 1 week ago

Question

★★★★★

=+c) Why did the researcher remove the Rent Index from the model?

Answered: 1 week ago

Question

★★★★★

Consider a seller who values a car at $9,500 and a buyer who values the same car at $10,000. What total surplus will result from a transaction between the two when the seller is faced with the...

Answered: 1 week ago

Question

★★★★★

Tom purchased 100 shares of Dalia Co. stock at a price of $125.58 four months ago. He sold all stocks today for $122.47. During the year the stock paid dividends of $6.71 per share. What is Toms...

Answered: 1 week ago

Question

★★★★★

The proposed rates were not in the range the CEO expected given the pricing analysis. The CEO has asked the pricing actuary to verify the total projected loss cost excluding potential large storm...

Answered: 1 week ago

Question

★★★★★

Ekasit, Inc. has 2 branches-Northern and Southern branches. The company's fixed costs that are traceable to the Northern branch is $175,000, while fixed costs that are traceable to the Southern...

Answered: 1 week ago

Question

★★★★★

1 In MS SQL we can calculate the email address for our vendor contacts IF the vendor has their email domain value provided in the VendorUpdates_20230107 table (not all of them do!). Email addresses...

Answered: 1 week ago

Question

★★★★★

Which brand, if any, emerged as the favorite? How did you determine this? 2 . Is the favorite generally a popular brand, or were you surprised by the winner? 3 . If a consumer had a favorite before...

Answered: 1 week ago

Question

★★★★★

An employer in Seattle, Washington has started a new "healthy lifestyle" initiative for employees and indpendent contractors. The desired achievement for each group is a mean score of 25 on a...

Answered: 1 week ago

Question

★★★★★

Bintang Jaya Bhd operates two (2) production departments, Machining, and Assembly and two (2) service departments, Canteen and Store. Machining department is highly dependent on the use of machines,...

Answered: 1 week ago

Question

★★★★★

Henrik is stopped behind another vehicle at an intersection. The light turns green, and he waits 3-4 seconds before accelerating. Why should he do this?It puts adequate following distance between...

Answered: 1 week ago

Question

★★★★★

Great the exercise's data is the following: Consider the knapsack problem ( linear programming problem ) : max z = 2 3 x 1 + 1 7 x 2 + 3 0 x 3 + 1 4 x 4 + 9 x 5 subject to 6 x 1 + 5 x 2 + 1 0 x 3 + 7...

Answered: 1 week ago

Question

★★★★★

Read the following description and Write a response of it. The discretion of public administrators can be decreased, but not altogether eliminated. Officials will use their discretion in any given...

Answered: 1 week ago

Question

★★★★★

Suppose that E and V are subsets of R with E bounded, V open, and V. Prove that there is a C function F: E R such that F(x) > 0 for x E and f(x) = 0 for V.

Answered: 1 week ago

Question

★★★★★

Suppose that f : [a, b] R. a) If f is not bounded above on [a, b], then given any partition P of [a, b] and M > 0, there exist tj [xj-1, xj] such that S(f, P, tj) > M. b) If the Riemann sums of f...

Answered: 1 week ago

Question

★★★★★

For each of the following, find S , where n is the outward-pointing normal. a) S is the topological boundary of the three-dimensional region enclosed by y = x2, z = 0, z = 1, y = 4, and = xyz dy dz...

Answered: 1 week ago

Question

★★★★★

Cardinal Ltd. is negotiating to lease a piece of equipment to MTBA plc. MTBA requests that the lease be for 9 years. The equipment has a useful life of 10 years. Cardinal wants a guarantee that the...

Answered: 1 week ago

Question

★★★★★

Assume that IBM (USA) leased equipment that was carried at a cost of 120,000 to Swander plc. The term of the lease is 6 years beginning December 31, 2018, with equal rental payments of 30,044...

Answered: 1 week ago

Question

★★★★★

Use the information for Escapee plc from BE21.18. Assume the same facts, except Escapee guarantees a residual value of 9,000 at the end of the lease term, which equals the expected residual value of...

Answered: 1 week ago

Previous Question Next Question