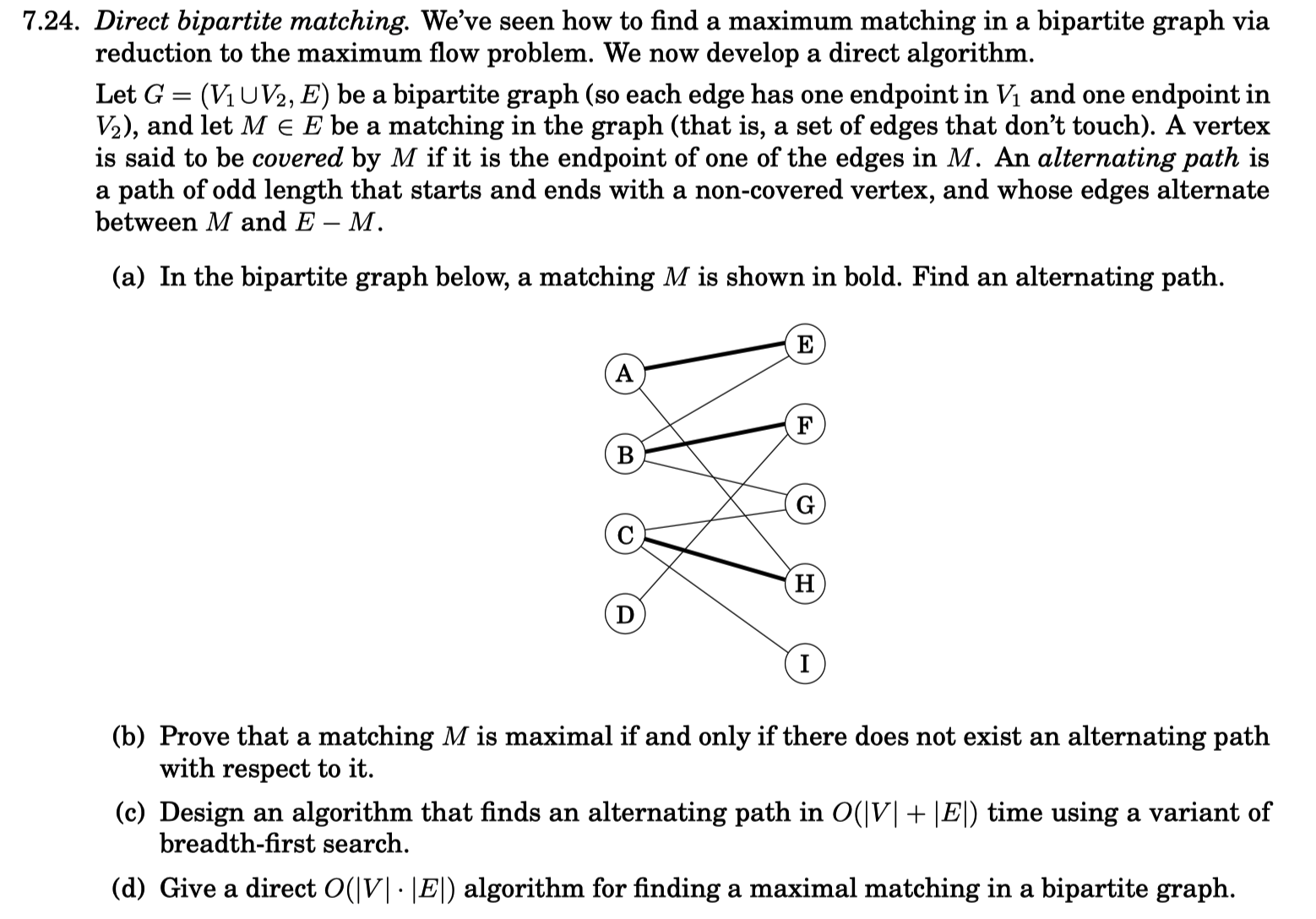
7.24. Direct bipartite matching. We've seen how to find a maximum matching in a bipartite graph via reduction to the maximum flow problem. We now develop a direct algorithm. Let G = (VUV2, E) be a bipartite graph (so each edge has one endpoint in V and one endpoint in V2), and let M = E be a matching in the graph (that is, a set of edges that don't touch). A vertex is said to be covered by M if it is the endpoint of one of the edges in M. An alternating path is a path of odd length that starts and ends with a non-covered vertex, and whose edges alternate between M and E - M. (a) In the bipartite graph below, a matching M is shown in bold. Find an alternating path. E A F B G H I (b) Prove that a matching M is maximal if and only if there does not exist an alternating path with respect to it. (c) Design an algorithm that finds an alternating path in O(|V| + |E|) time using a variant of breadth-first search. (d) Give a direct O(|V| |E|) algorithm for finding a maximal matching in a bipartite graph.