7.5.16 only: inferences based on the normal distribution-drawing inferences about lower case sigma squared

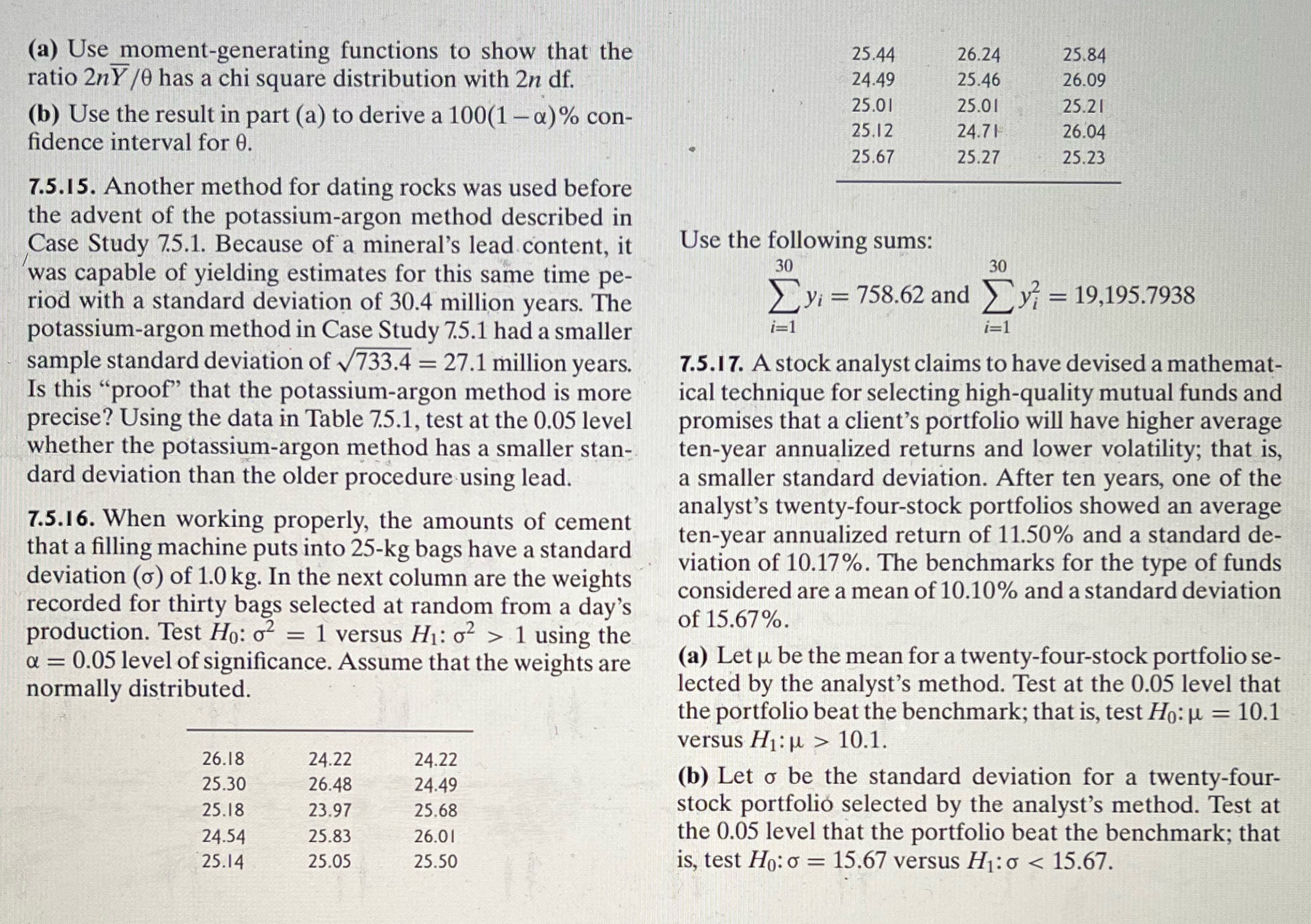
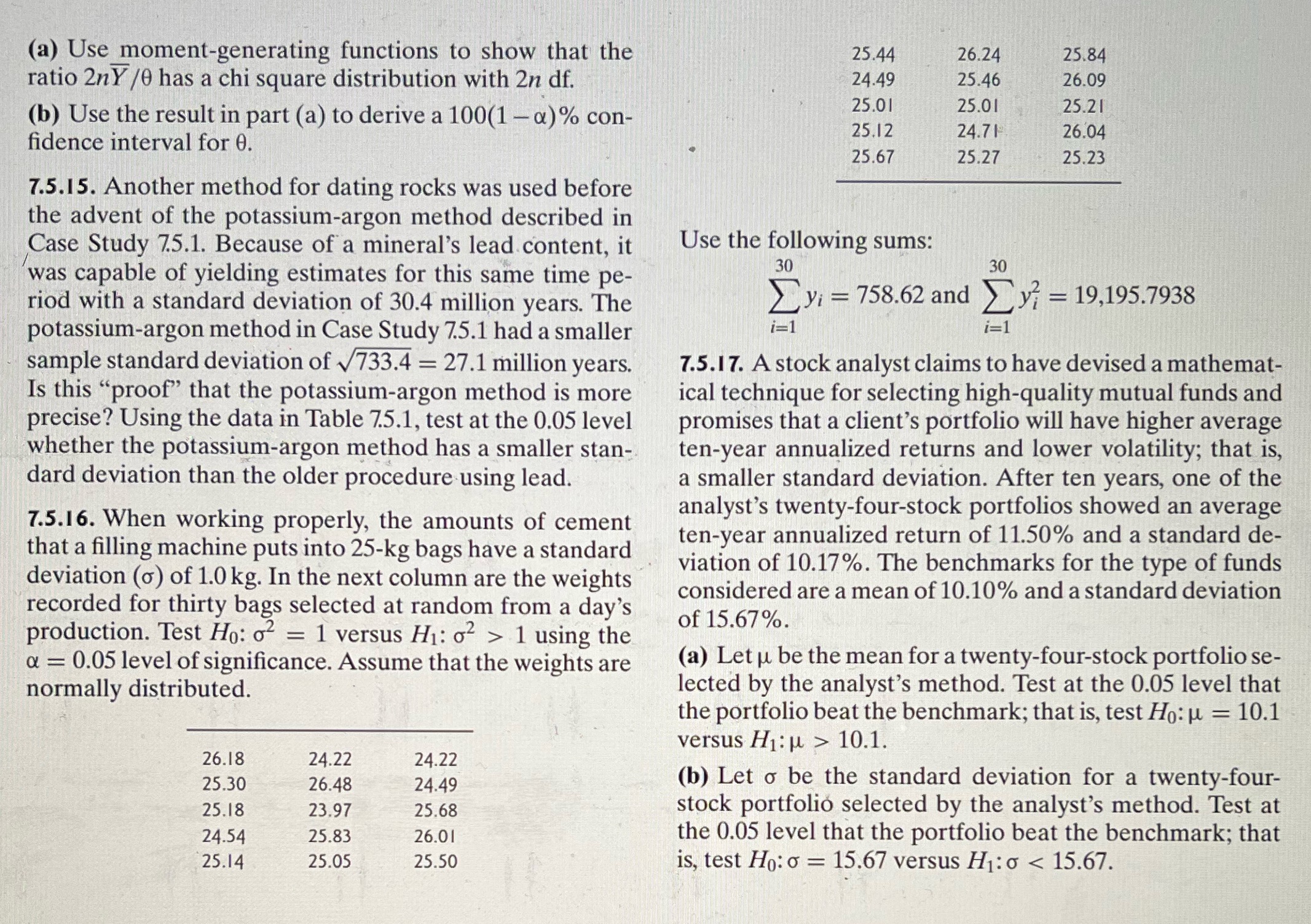
(a) Use moment-generating functions to show that the 25.44 26.24 25.84 ratio 2nY /0 has a chi square distribution with 2n df. 24.49 25.46 26.09 (b) Use the result in part (a) to derive a 100(1 -a) % con- 25.01 25.01 25.21 25.12 24.71 26.04 fidence interval for 0. 25.67 25.27 25.23 7.5.15. Another method for dating rocks was used before the advent of the potassium-argon method described in Case Study 7.5.1. Because of a mineral's lead content, it Use the following sums: was capable of yielding estimates for this same time pe- 30 30 riod with a standard deviation of 30.4 million years. The Evi = 758.62 and Ey? = 19,195.7938 potassium-argon method in Case Study 7.5.1 had a smaller i=1 sample standard deviation of v733.4 = 27.1 million years. 7.5.17. A stock analyst claims to have devised a mathemat- Is this "proof" that the potassium-argon method is more ical technique for selecting high-quality mutual funds and precise? Using the data in Table 7.5.1, test at the 0.05 level promises that a client's portfolio will have higher average whether the potassium-argon method has a smaller stan- ten-year annualized returns and lower volatility; that is, dard deviation than the older procedure using lead. a smaller standard deviation. After ten years, one of the 7.5.16. When working properly, the amounts of cement analyst's twenty-four-stock portfolios showed an average that a filling machine puts into 25-kg bags have a standard ten-year annualized return of 11.50% and a standard de- deviation () of 1.0 kg. In the next column are the weights viation of 10.17%. The benchmarks for the type of funds recorded for thirty bags selected at random from a day's considered are a mean of 10.10% and a standard deviation production. Test Ho: 02 = 1 versus H1: o2 > 1 using the of 15.67%. a = 0.05 level of significance. Assume that the weights are (a) Let u be the mean for a twenty-four-stock portfolio se- normally distributed. lected by the analyst's method. Test at the 0.05 level that the portfolio beat the benchmark; that is, test Ho: ul = 10.1 versus Hip > 10.1. 26.18 24.22 24.22 25.30 26.48 24.49 (b) Let o be the standard deviation for a twenty-four- 25.18 23.97 25.68 stock portfolio selected by the analyst's method. Test at 24.54 25.83 26.01 the 0.05 level that the portfolio beat the benchmark; that 25.14 25.05 25.50 is, test Ho:o = 15.67 versus H1:0