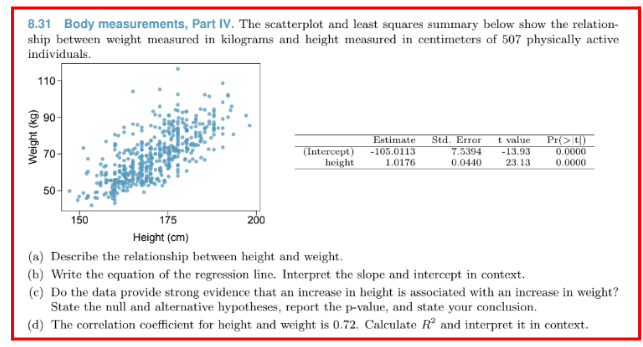
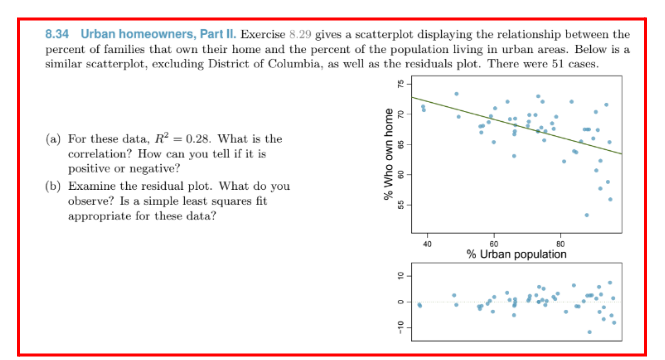
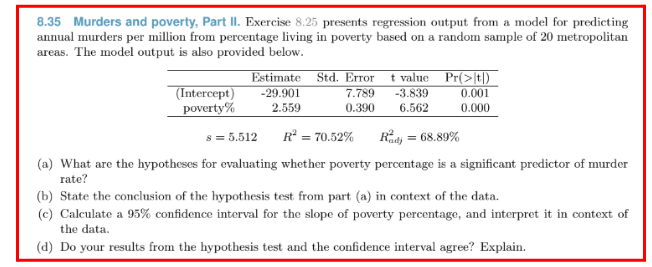
8.31 Body measurements, Part IV. The scatterplot and least squares summary below show the relation- ship between weight measured in kilograms and height measured in centimeters of 507 physically active individuals. Weight (kg) 110- 90- 70- 70 (Intercept) height Estimate Std. Error -105.0113 1.0176 7.5394 0.0440 t value -13.93 Pr(>t) 0.0000 23.13 0.0000 50-- 150 175 Height (cm) 200 (a) Describe the relationship between height and weight. (b) Write the equation of the regression line. Interpret the slope and intercept in context. (c) Do the data provide strong evidence that an increase in height is associated with an increase in weight? State the null and alternative hypotheses, report the p-value, and state your conclusion. (d) The correlation coefficient for height and weight is 0.72. Calculate R and interpret it in context. 8.34 Urban homeowners, Part II. Exercise 8.29 gives a scatterplot displaying the relationship between the percent of families that own their home and the percent of the population living in urban areas. Below is a similar scatterplot, excluding District of Columbia, as well as the residuals plot. There were 51 cases. (a) For these data, R2 = 0.28. What is the correlation? How can you tell if it is positive or negative? (b) Examine the residual plot. What do you observe? Is a simple least squares fit appropriate for these data? 55 % Who own home 09 65 10 2- 40 60 80 % Urban population 8.35 Murders and poverty, Part II. Exercise 8.25 presents regression output from a model for predicting annual murders per million from percentage living in poverty based on a random sample of 20 metropolitan areas. The model output is also provided below. Estimate Std. Error t value Pr(>|t|) (Intercept) poverty% -29.901 2.559 7.789 -3.839 0.001 0.390 6.562 0.000 8 = 5.512 R = 70.52% Rady = 68.89% (a) What are the hypotheses for evaluating whether poverty percentage is a significant predictor of murder rate? (b) State the conclusion of the hypothesis test from part (a) in context of the data. (c) Calculate a 95% confidence interval for the slope of poverty percentage, and interpret it in context of the data. (d) Do your results from the hypothesis test and the confidence interval agree? Explain.