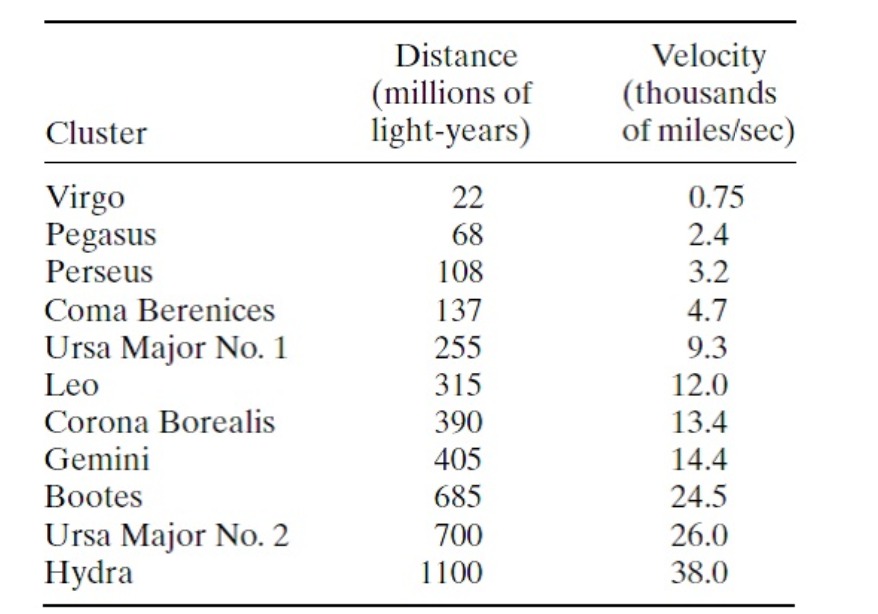
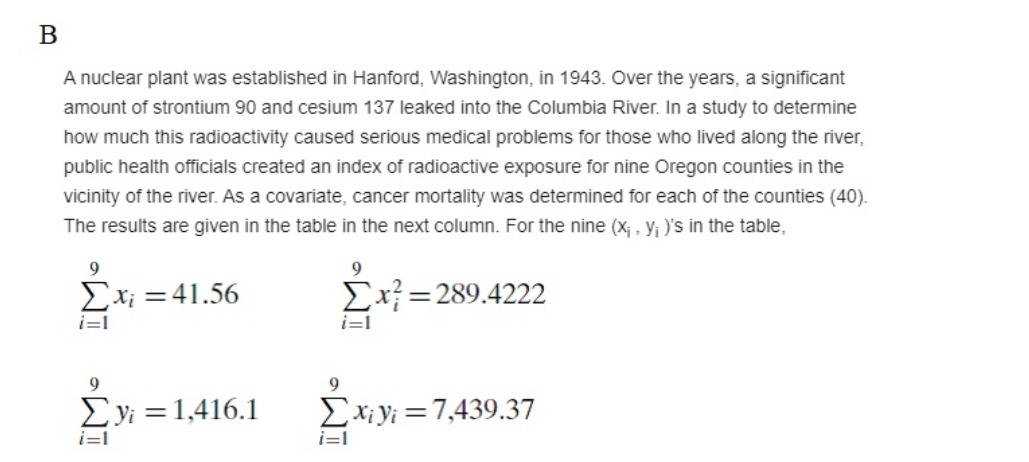A (a) Find the equation of the least squares straight line for the plant cover diversity/bird species diversity data given in Question 8.2.11. (b) Make the residual plot associated with the least squares fit asked for in part (a). Based on the appearance of the residual plot, would you conclude that fitting a straight line to these data is appropriate? Explain. Reference: Question 8.2.11: When two closely related species are crossed, the progeny will tend to have physical traits that lie somewhere between those of the two parents. Whether a similar mixing occurs with behavioral traits was the focus of an experiment where the subjects were mallard and pintail ducks (162). A total of eleven males were studied; all were second-generation crosses. A rating scale was devised that measured the extent to which the plumage of each of the ducks resembled the plumage of the first generation's parents. A score of 0 indicated that the hybrid had the same appearance (phenotype) as a pure mallard; a score of 20 meant that the hybrid looked like a pintail. Similarly, certain behavioral traits were quantified and a second scale was constructed that ranged from 0 (completely mallard-like) to 15 (completely pintail-like). Use Theorem 11.2.1 and the following data to summarize the relationship between the plumage and behavioral indices. Does a linear model seem adequate?A nuclear plant was established in Hanford. washington, in 1943. Over the years, a signicant amount of strontium 90 and cesium 137 leaked into the Columbia River. In a study to determine how much this radioactivity caused serious medical problems for those who lived along the river. public heatth otcials created an index of radioactive exposure for nine Oregon counties in the vicinity of the river. As a covariate, cancer mortality was determined for each of the counties (40). The results are given in the table in the next column. For the n'me (xi . y,- )'s in the table, 9 9 2x.- :41 .56 2x? =289.4222 i=1 9 9 E y: = 1,416.1 Z xgy; = 7,439.37 i=1 r':l C) When two closely related species are crossed, the progeny will tend to have physical traits that lie somewhere between those of the two parents. Whether a similar mixing occurs with behavioral traits was the focus of an experiment where the subjects were mallard and pintail ducks (162). A total of eleven males were studied; all were second-generation crosses. A rating scale was devised that measured the extent to which the plumage of each of the ducks resembled the plumage of the first generation's parents. A score of 0 indicated that the hybrid had the same appearance (phenotype) as a pure mallard; a score of 20 meant that the hybrid looked like a pintail. Similarly, certain behavioral traits were quantified and a second scale was constructed that ranged from 0 (completely mallard-like) to 15 (completely pintail-like). Use Theorem 11.2.1 and the following data to summarize the relationship between the plumage and behavioral indices. Does a linear model seem adequate?D) In some l'Egl'BSSiOI'I situations, there are a DFFOH reasons for assuming that the Jar-relationship being approximated passes through the origin. If so, the equation to be t to the (xi , yi )'s has the form y =bx. Use the least squares criterion to show that the \"best" slope in that case is given by Ext): = i=1 2x: I) B) One of the most startling scientific discoveries of the twentieth century was the announcement in 1929 by the American astronomer Edwin Hubble that the universe is expanding- If v is a galaxy's recession velocity (relative to that of any other galaxy) and d is its distance (from that same galaxy), Hubble's law states that v=Hd where H is Known as Hubble's constant (T o cosmologists, Hubble's constant is a critically important numberits reciprocal, after being progeny scaled, is an estimate of the age of the universe.) The following are distance and velocity measurements made on eleven galactic clusters (23). Use the formula cited in Question 11.2.14 to estimate Hubble's constant. Distance Velocity (millions of (thousands Cluster light-years) of miles/sec) Virgo 22 0.75 Pegasus 68 2.4 Perseus 108 3.2 Coma Berenices 137 4.7 Ursa Major No. 1 255 9.3 Leo 315 12.0 Corona Borealis 390 13.4 Gemini 405 14.4 Bootes 685 24.5 Ursa Major No. 2 700 26.0 Hydra 1100 38.0Reference: Question 11.2.14: In some regression situations, there are a priori reasons for assuming that the xy-relationship being approximated passes through the origin. If so, the equation to be fit to the (x; , y; )'s has the form y =bx. Use the least squares criterion to show that the "best" slope in that case is given by n xi yi b = i=1 n i=1 F Given a set of n linearly related points, (X1, y1). (X2. Y2). . . . . and (Xn, yn), use the least squares criterion to find formulas for (a) a if the slope of the xy-relationship is known to be b*. (b) b if the y-intercept of the xy-relationship is known to be a"