(a) Assume a binomial distribution with parameter p:

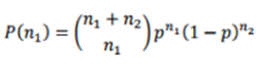
We want to estimate the parameter p which is P(outcome 1). Assume you have a training set of n data points of which n ₁ are outcome 1 and n ₂ are outcome 2. Derive the maximum likelihood estimator for p given these data.

(b) Recall that the beta distribution is the conjugate prior for the binomial.

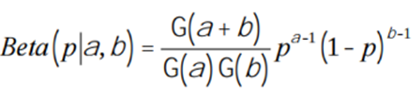
Show that if the prior probability of p follows a beta with parameters (u.[) and the likelihood of p given the data set from (a) follows a binomial, the posterior probability of p given the data set is a beta distribution with parameters (N ₁ + ?, N2 + (?)

(c) Given a posterior distribution of p that follows beta(?, (?), derive the expected value of p.

Transcribed Image Text:

P(n₂) = (1+2) p²¹ (1-p)" G(a+b) a-1 Beta (pla, b) = G(a) G(b) p²¹ (1-p)²-1 P(n₂) = (1+2) p²¹ (1-p)" G(a+b) a-1 Beta (pla, b) = G(a) G(b) p²¹ (1-p)²-1

Answer rating: 100% (QA)

a To find MLE of p we maximize the likel... View the full answer