A. Based on the information below, and assuming a range of 11-13% WACC and 3-5% terminal value growth rate, what is the range of values for Saito Solar?
B.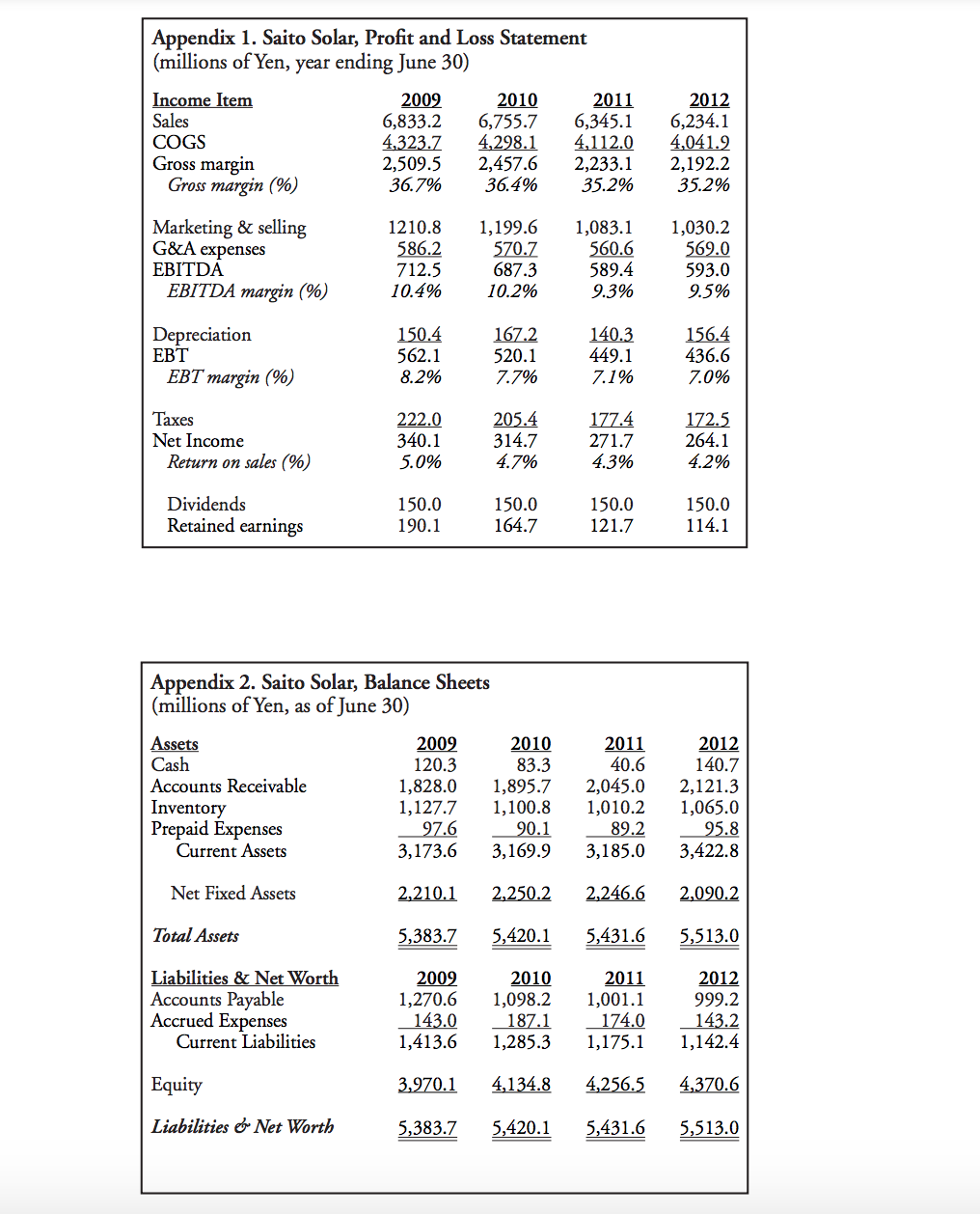 
Strategically, do you think Mr. Saito and his partners should sell the firm at this time?
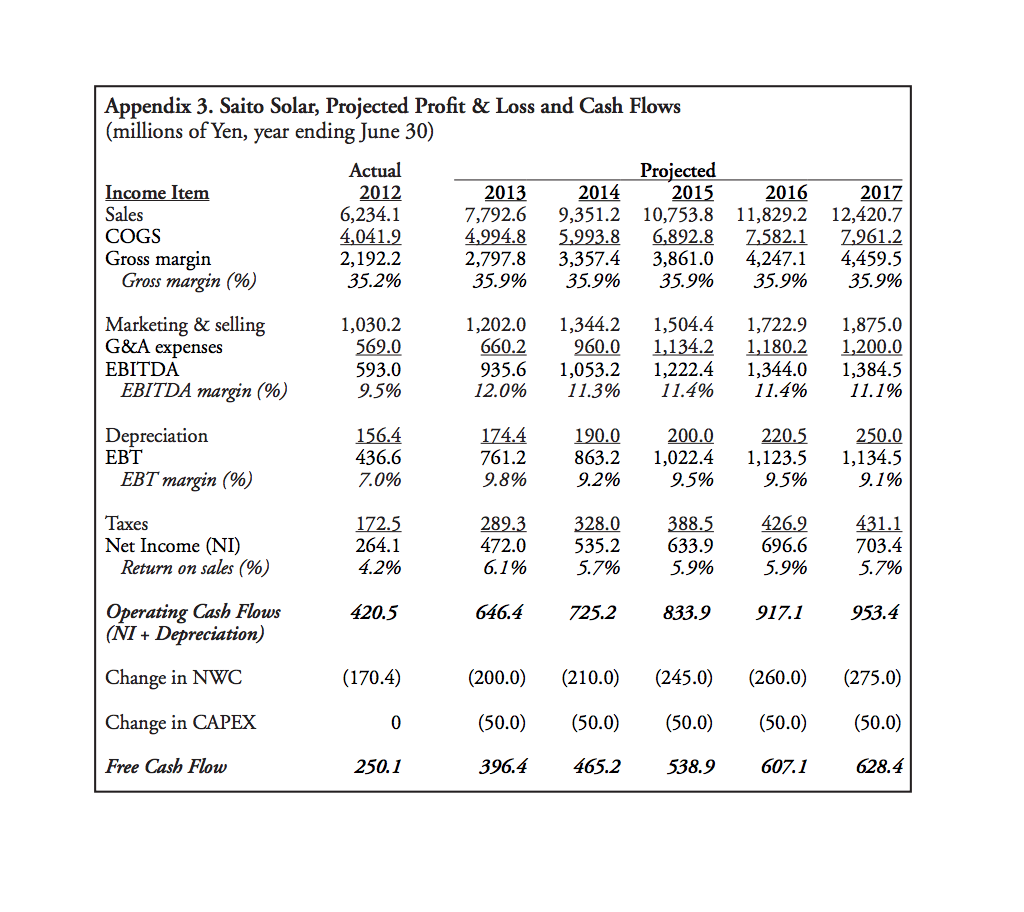
Appendix 1. Saito Solar, Profit and Loss Statement (millions of Yen, year ending June 30) Income Item 2009 2010 2011 Sales 6,833.2 6,755.7 6,345.1 COGS 4,323.7 4,298.1 4,112.0 Gross margin 2,509.5 2,457.6 2,233.1 Gross margin (%) 36.7% 36.4% 35.2% 2012 6,234.1 4,041.9 2,192.2 35.2% Marketing & selling G&A expenses EBITDA EBITDA margin (%) 1210.8 586.2 712.5 10.4% 1,199.6 570.7 687.3 10.2% 1,083.1 560.6 589.4 9.3% 1,030.2 569.0 593.0 9.5% Depreciation EBT EBT margin (%) 150.4 562.1 8.2% 167.2 520.1 7.7% 140.3 449.1 7.1% 156.4 436.6 7.0% Taxes Net Income Return on sales (%) 222.0 340.1 5.0% 205.4 314.7 4.7% 177.4 271.7 4.3% 172.5 264.1 4.2% Dividends Retained earnings 150.0 190.1 150.0 164.7 150.0 121.7 150.0 114.1 Appendix 2. Saito Solar, Balance Sheets (millions of Yen, as of June 30) Assets Cash Accounts Receivable Inventory Prepaid Expenses Current Assets 2009 120.3 1,828.0 1,127.7 97.6 3,173.6 2010 83.3 1,895.7 1,100.8 90.1 3,169.9 2011 40.6 2,045.0 1,010.2 89.2 3,185.0 2012 140.7 2,121.3 1,065.0 95.8 3,422.8 Net Fixed Assets 2,210.1 2,250.2 2.246.6 2,090.2 Total Assets 5,383.7 5,420.1 5,431.6 5,513.0 2012 Liabilities & Net Worth Accounts Payable Accrued Expenses Current Liabilities 2009 1,270.6 143.0 1,413.6 2010 1,098.2 187.1 1,285.3 2011 1,001.1 174.0 1,175.1 999.2 143.2 1,142.4 Equity 3,970.1 4,134.8 4,256.5 4,370.6 Liabilities & Net Worth 5,383.7 5,420.1 5,431.6 5,513.0 Appendix 3. Saito Solar, Projected Profit & Loss and Cash Flows (millions of Yen, year ending June 30) Actual Projected Income Item 2012 2013 2014 2015 Sales 6,234.1 7,792.6 9,351.2 10,753.8 COGS 4,041.9 4,994.8 5.993.8 6,892.8 Gross margin 2,192.2 2,797.8 3,357.4 3,861.0 Gross margin (%) 35.2% 35.9% 35.9% 35.9% 2016 11,829.2 7.582.1 4,247.1 35.9% 2017 12,420.7 7,961.2 4,459.5 35.9% Marketing & selling G&A expenses EBITDA EBITDA margin (%) 1,030.2 569.0 593.0 9.5% 1,202.0 660.2 935.6 12.0% 1,344.2 960.0 1,053.2 11.3% 1,504.4 1,134.2 1,222.4 11.4% 1,722.9 1,180.2 1,344.0 11.4% 1,875.0 1,200.0 1,384.5 11.1% Depreciation EBT EBT margin (%) 156.4 436.6 7.0% 174.4 761.2 9.8% 190.0 863.2 9.2% 200.0 1,022.4 9.5% 220.5 1,123.5 9.5% 250.0 1,134.5 9.1% Taxes Net Income (NI) Return on sales (%) 172.5 264.1 289.3 472.0 6.1% 328.0 535.2 5.7% 388.5 633.9 5.9% 426.2 696.6 431.1 703.4 5.7% 4.2% 5.9% 420.5 646.4 725.2 833.9 917.1 953.4 Operating Cash Flows (NI + Depreciation) Change in NWC (170.4) (200.0) (210.0) (245.0) (260.0) (275.0) Change in CAPEX 0 (50.0) (50.0) (50.0) (50.0) (50.0) Free Cash Flow 250.1 396.4 465.2 538.9 607.1 628.4 Appendix 4. Discounting Future Cash Flows with Formulas A firm's free cash flows can be in a variety of patterns, ranging from a simple single future cash flow to a complex mixed stream of projected cash flows. Most, if not all, can be handled by one of the formulas below. Generic DCF Formula CF PV = *(1+r) PV = the present value of the cash flow stream CFt - the cash flow which occurs at the end of year t . 1 = the discount rate assumed to be constant over the project horizon) . t= the year, which ranges from one to n n = the last year in which a cash flow occurs denotes summation of the cash flows as t goes from 1 ton Note that discount rate, opportunity rate, required rate of return, interest rate, capitalization rate, and weighted average cost of capital (WACC) are terms used interchangeably by authors and practitioners. Fortunately, simpler versions (shortcuts) of the above formula exist, including: No Growth Perpetuity CF PV = where CF is the constant perpetual cash flow and r = the discount rate. Growing Perpetuity CF PV = r-g where CF, is the cash flow at the end of year one, r = the discount rate, and g = the growth rate. Regular Annuity 1 PV = CFC r r(1+r)' where CF represents the steady end-of-year cash flow, r = the discount rate, and T = the number of constant cash flows. The term in brackets is defined as an annuity factor, and facilitates more tedious algebraic computation. Growing Annuity PV = C r-g 1- 1+g 1+1 where r = the discount rate, g = the growth rate, and T = the number of cash flows. Note that the formula above is simply the PV of a growing perpetuity penalized by cash flows foregone. In all of these cases, cash flows are assumed to occur at the end of the year, and the formulas throughout represent discrete (vs. continuous) time versions of these cash flows
