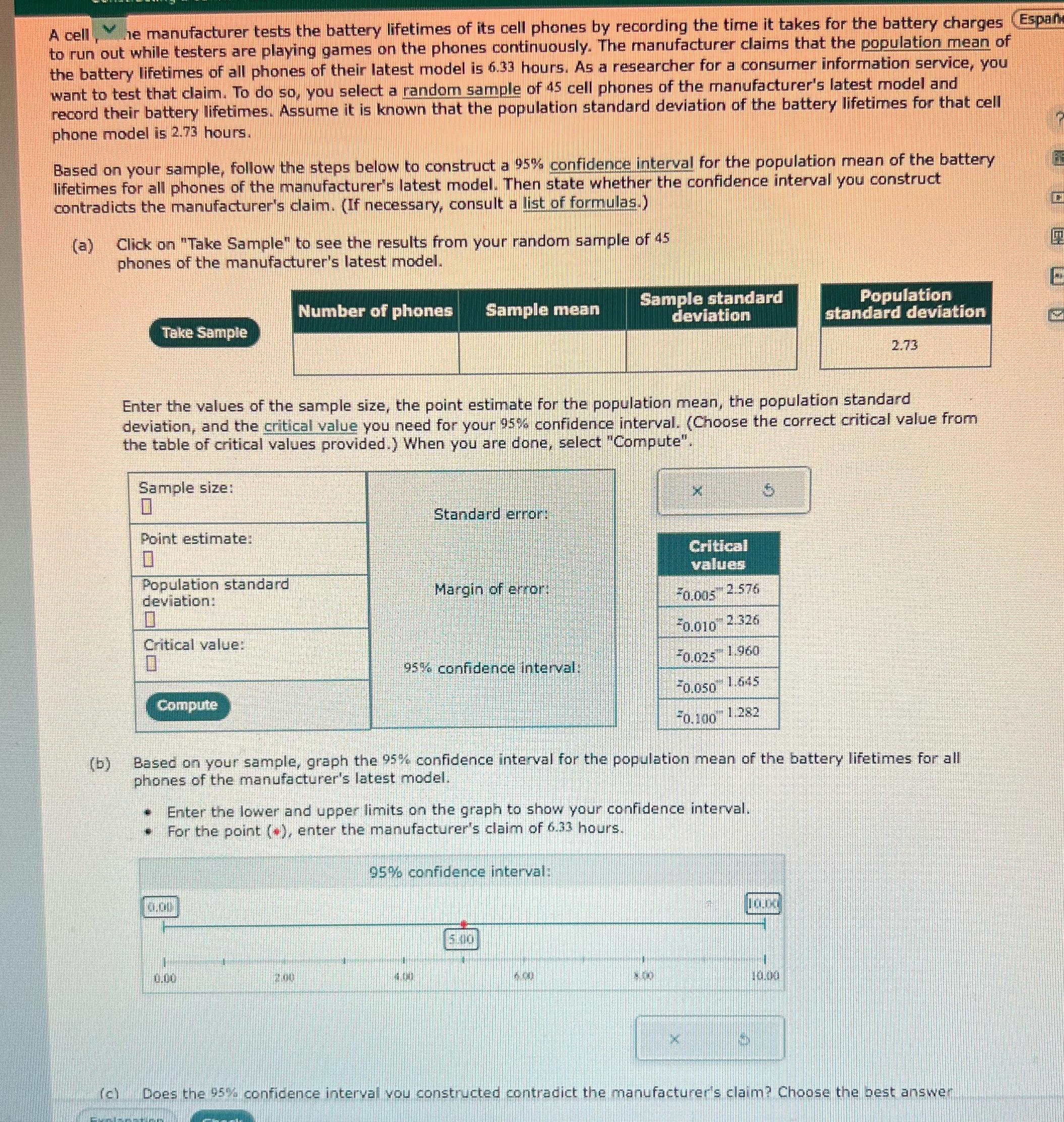
A cell , hilhe manufacturer tests the battery lifetimes of its cell phones by recording the time it takes for the battery charges (Espar to run out while testers are playing games on the phones continuously. The manufacturer claims that the population mean of the battery lifetimes of all phones of their latest model is 6.33 hours. As a researcher for a consumer information service, you want to test that claim. To do so, you select a random sample of 45 cell phones of the manufacturer's latest model and record their battery lifetimes. Assume it is known that the population standard deviation of the battery lifetimes for that cell phone model is 2.73 hours. Based on your sample, follow the steps below to construct a 95%% confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. Then state whether the confidence interval you construct contradicts the manufacturer's claim. (If necessary, consult a list of formulas.) (a) Click on "Take Sample" to see the results from your random sample of 45 phones of the manufacturer's latest model. Number of phones Sample mean Sample standard Population deviation standard deviation Take Sample 2.73 Enter the values of the sample size, the point estimate for the population mean, the population standard deviation, and the critical value you need for your 95%% confidence interval. (Choose the correct critical value from the table of critical values provided.) When you are done, select "Compute". Sample size: Standard error: Point estimate: Critical values Population standard deviation: Margin of error 50.005 2-576 0.010 2.326 Critical value: 50.025- 1.960 95% confidence interval Fo.050 1.645 Compute Zo.100 1.282 (b) Based on your sample, graph the 95%% confidence interval for the population mean of the battery lifetimes for all phones of the manufacturer's latest model. Enter the lower and upper limits on the graph to show your confidence interval For the point ("), enter the manufacturer's claim of 6.33 hours. 95% confidence interval: 5.00 0.00 (c) Does the 95%% confidence interval you constructed contradict the manufacturer's claim? Choose the best