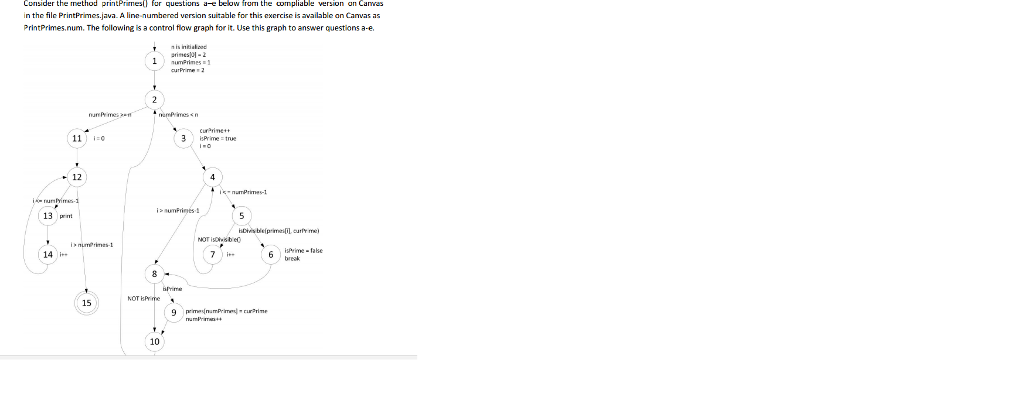
Question
(a) Consider test cases t1 = (n = 3) and t2 = (n = 5). Although these tour the same prime paths in printPrimes(), they
(a) Consider test cases t1 = (n = 3) and t2 = (n = 5). Although these tour the same prime paths in printPrimes(), they do not necessarily find the same faults. Design a simple fault that t2 would be more likely to discover than t1 would. (2 points)
(b) For printPrimes(), find a test case such that the corresponding test path visits the edge that connects the beginning of the while statement to the for statement without going through the body of the while loop. ( 2 points)'
(c) List the test requirements for Node Coverage (1 point), and Edge Coverage (9 points)
(d) List test paths that achieve Node Coverage but not Edge Coverage on the graph. (2 points)
(e) List test paths that achieve Edge Coverage but not Prime Path Coverage on the graph. (2 points)
public class PrintPrimes {
private static boolean isDivisible (int i, int j) { if (j%i == 0) return true; else return false; } private static void printPrimes (int n) { int curPrime; // Value currently considered for primeness int numPrimes; // Number of primes found so far. boolean isPrime; // Is curPrime prime? int [] primes = new int [100]; // The list of prime numbers. // Initialize 2 into the list of primes. primes [0] = 2; numPrimes = 1; curPrime = 2; while (numPrimes
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


