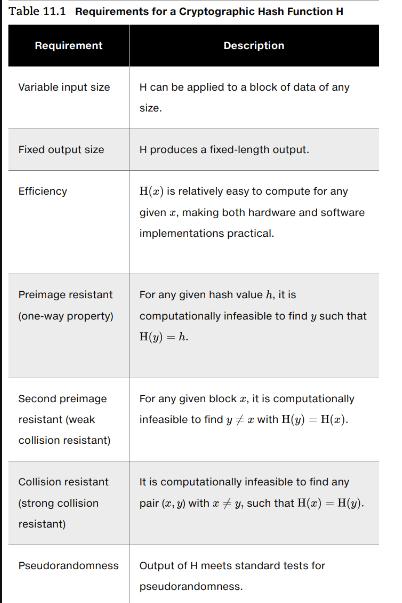
a. Consider the following hash function. Messages are in the form of a sequence of numbers in Zn, M (a1, a2, = at). The hash value h is calculated for some predefined value n. Does this hash as ... function satisfy any of the requirements for a hash function listed in Table 11.1? Explain your answer. b. Repeat part (a) for the hash function -( (0)) c. Calculate the hash function of part (b) for M = (189, 632, 900, 722, 349) and n = 989. h = mod n. Table 11.1 Requirements for a Cryptographic Hash Function H Requirement Variable input size Fixed output size Efficiency Preimage resistant (one-way property) Second preimage resistant (weak collision resistant) Collision resistant (strong collision resistant) Pseudorandomness Description H can be applied to a block of data of any size. H produces a fixed-length output. H() is relatively easy to compute for any given , making both hardware and software implementations practical. For any given hash value h, it is computationally infeasible to find y such that H(y) =h. For any given block z, it is computationally infeasible to find y + z with H(y) = H (z). # It is computationally infeasible to find any pair (x,y) with #y, such that H(x) - H(y). x Output of H meets standard tests for pseudorandomness.