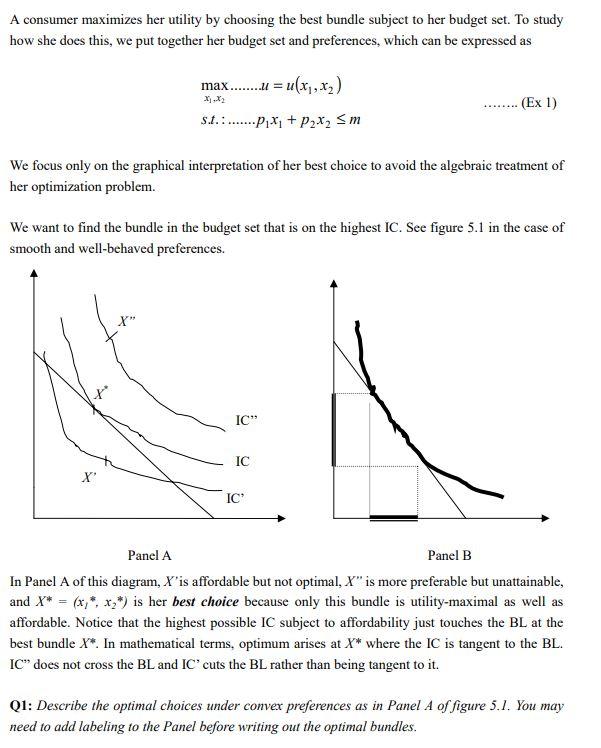
A consumer maximizes her utility by choosing the best bundle subject to her budget set. To study how she does this, we put together her budget set and preferences, which can be expressed as maxx1,x2.u=u(x1,x2)s.t.:......p1x1+p2x2m We focus only on the graphical interpretation of her best choice to avoid the algebraic treatment of her optimization problem. We want to find the bundle in the budget set that is on the highest IC. See figure 5.1 in the case of smooth and well-behaved preferences. Panel A Panel B In Panel A of this diagram, X is affordable but not optimal, X is more preferable but unattainable, and X=(xl,x2) is her best choice because only this bundle is utility-maximal as well as affordable. Notice that the highest possible IC subject to affordability just touches the BL at the best bundle X. In mathematical terms, optimum arises at X where the IC is tangent to the BL. IC' does not cross the BL and IC' cuts the BL rather than being tangent to it. Q1: Describe the optimal choices under convex preferences as in Panel A of figure 5.1. You may need to add labeling to the Panel before writing out the optimal bundles. A consumer maximizes her utility by choosing the best bundle subject to her budget set. To study how she does this, we put together her budget set and preferences, which can be expressed as maxx1,x2.u=u(x1,x2)s.t.:......p1x1+p2x2m We focus only on the graphical interpretation of her best choice to avoid the algebraic treatment of her optimization problem. We want to find the bundle in the budget set that is on the highest IC. See figure 5.1 in the case of smooth and well-behaved preferences. Panel A Panel B In Panel A of this diagram, X is affordable but not optimal, X is more preferable but unattainable, and X=(xl,x2) is her best choice because only this bundle is utility-maximal as well as affordable. Notice that the highest possible IC subject to affordability just touches the BL at the best bundle X. In mathematical terms, optimum arises at X where the IC is tangent to the BL. IC' does not cross the BL and IC' cuts the BL rather than being tangent to it. Q1: Describe the optimal choices under convex preferences as in Panel A of figure 5.1. You may need to add labeling to the Panel before writing out the optimal bundles