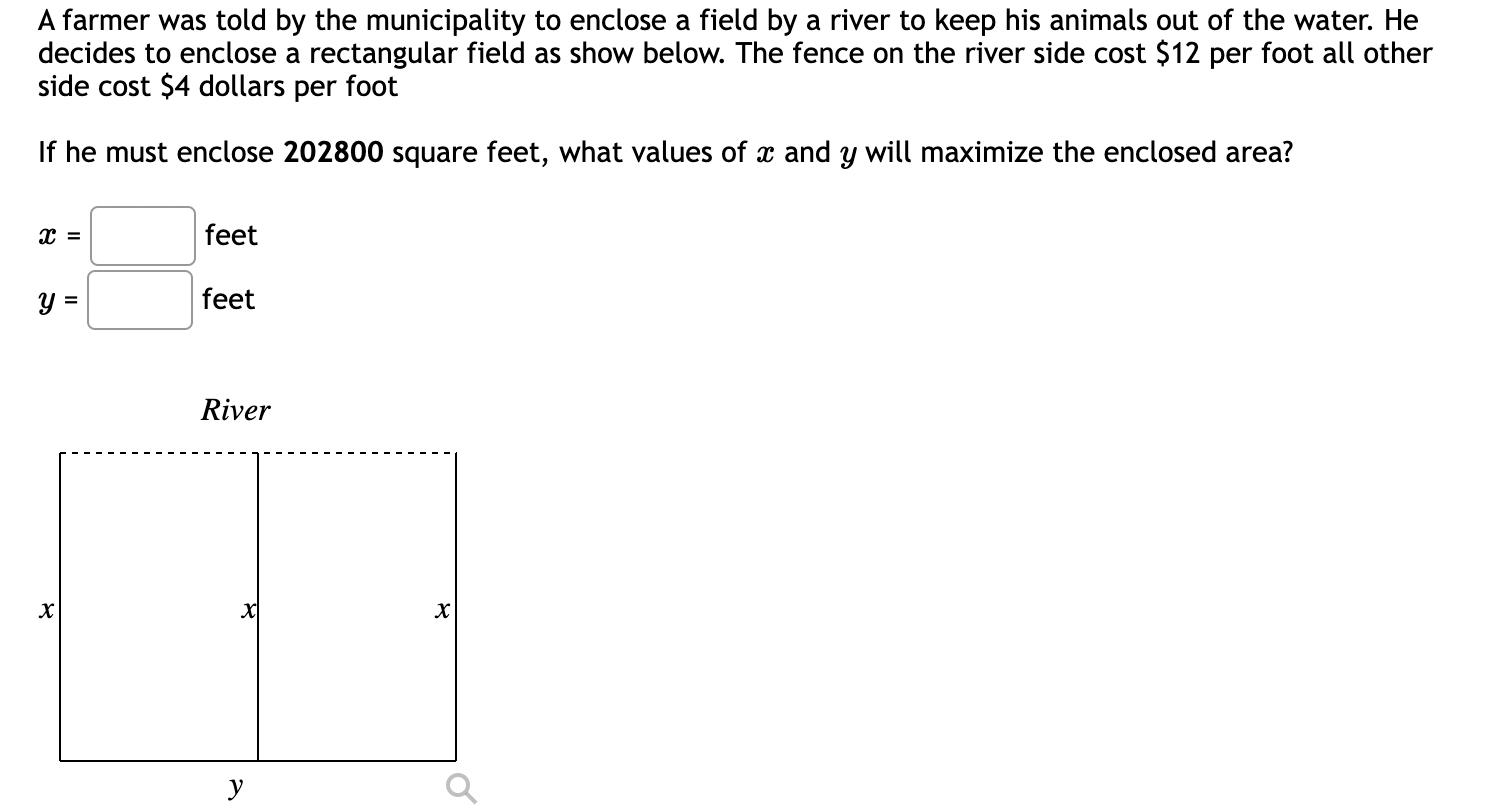
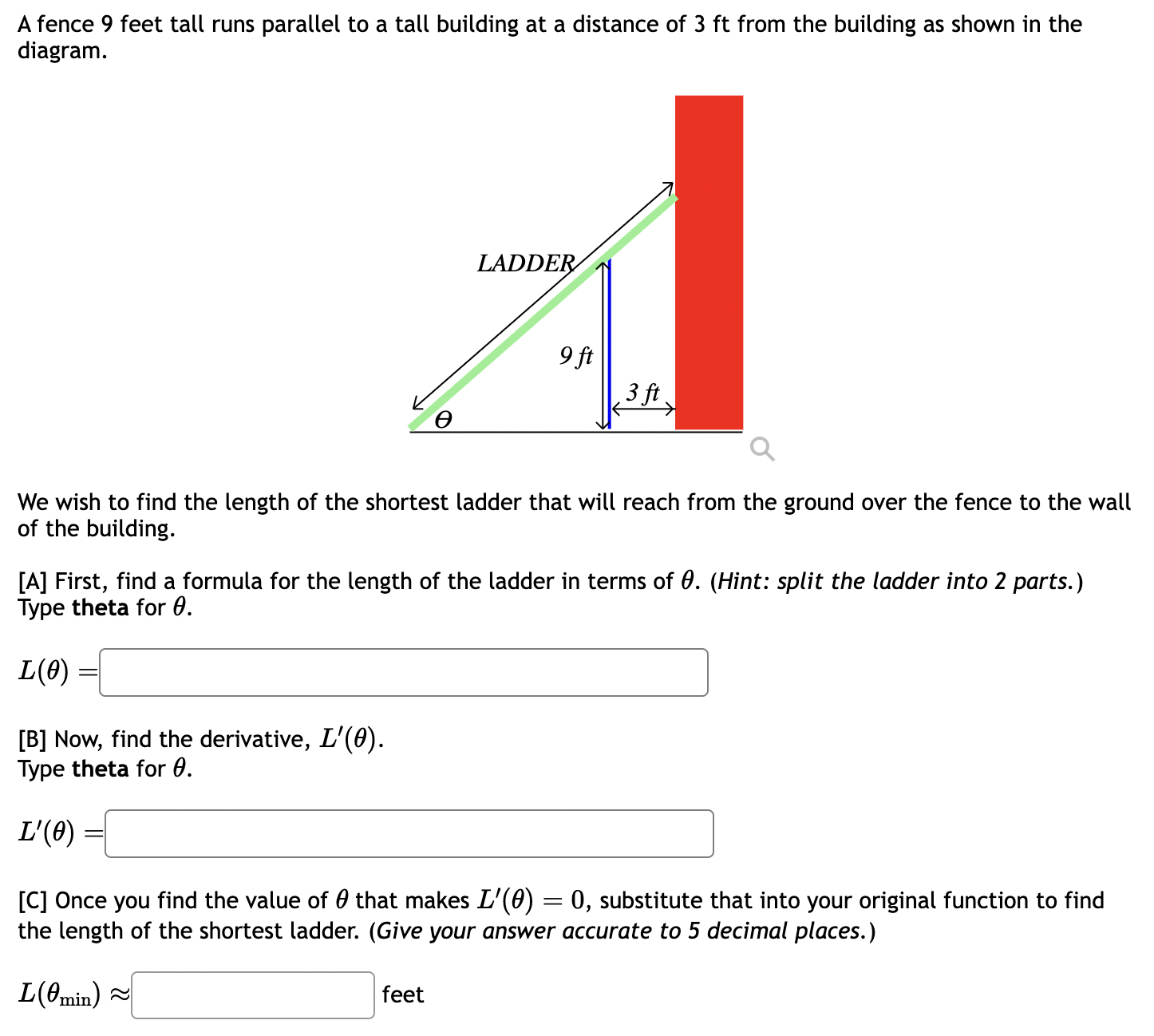
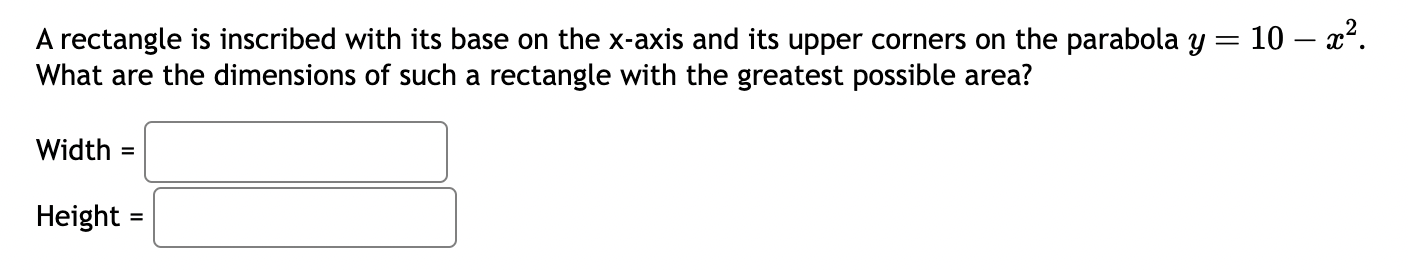
A farmer is setting up separate pens for livestock by fencing off a rectangular area and running fence to create four parallel pens. If the farmer has a total of 500 yards of fence, what is the largest area that can be contained? Area = square yards A farmer is setting up separate pens for livestock by fencing off a rectangular area and running fence to create seven parallel pens. If the farmer has to enclose a total area of 1,600 square yards, what is the shortest length of fence needed? Total fence length = yards Open-box Problem. An open-box (top open) is made from a rectangular material of dimensions a = 14 inches by b = 11 inches by cutting a square of side x at each corner and turning up the sides (see the figure). Determine the value of x that results in a box the maximum volume. 12 10 987 A 2- + 7 8 b 10 11 12 13 14 15 Following the steps to solve the problem. Check Show Answer only after you have tried hard. (1) Express the volume V as a function of x: V = (2) Determine the domain of the function V of x (in interval form): (3) Expand the function V for easier differentiation: V = = (4) Find the derivative of the function V: V'= (5) Find the critical point(s) in the domain of V: (6) The value of V at the left endpoint is (7) The value of V at the right endpoint is (8) The maximum volume is V: = A piece of cardboard measuring 9 inches by 10 inches is formed into an open-top box by cutting squares with side length x from each corner and folding up the sides. Find a formula for the volume of the box in terms of x V(x) = Find the value for x that will maximize the volume of the box x = A box with a square base and open top must have a volume of 470596 cm. We wish to find the dimensions of the box that minimize the amount of material used. First, find a formula for the surface area of the box in terms of only x, the length of one side of the square base. [Hint: use the volume formula to express the height of the box in terms of x.] Simplify your formula as much as possible. A(x) = Next, find the derivative, A'(x). A'(x) Now, calculate when the derivative equals zero, that is, when A'(x) = 0. [Hint: multiply both sides by x .] A'(x) = 0 when x We next have to make sure that this value of x gives a minimum value for the surface area. Let's use the second derivative test. Find A"(x). A"(x) Evaluate A"(x) at the x-value you gave above. NOTE: Since your last answer is positive, this means that the graph of A(x) is concave up around that value, so the zero of A'(x) must indicate a local minimum for A(x). (Your boss is happy now.) If 2100 square centimeters of material is available to make a box with a square base and an open top, find the largest possible volume of the box. Volume: = cubic centimeters. A farmer was told by the municipality to enclose a field by a river to keep his animals out of the water. He decides to enclose a rectangular field as show below. The fence on the river side cost $12 per foot all other side cost $4 dollars per foot If he must enclose 202800 square feet, what values of x and y will maximize the enclosed area? x = feet y = feet River x X x y Q A fence 9 feet tall runs parallel to a tall building at a distance of 3 ft from the building as shown in the diagram. LADDER 9 ft 3 ft. We wish to find the length of the shortest ladder that will reach from the ground over the fence to the wall of the building. [A] First, find a formula for the length of the ladder in terms of 0. (Hint: split the ladder into 2 parts.) Type theta for 0. L(0) [B] Now, find the derivative, L'(0). Type theta for 0. L'(0) [C] Once you find the value of 0 that makes L'(0) = 0, substitute that into your original function to find the length of the shortest ladder. (Give your answer accurate to 5 decimal places.) L(0 min) ~ feet A rectangle is inscribed with its base on the x-axis and its upper corners on the parabola y = 10 - x. What are the dimensions of such a rectangle with the greatest possible area? Width = Height =