Question: (a) For a group G and g E G let c : GG be defined by ca(r) =gg for all x G. Prove that

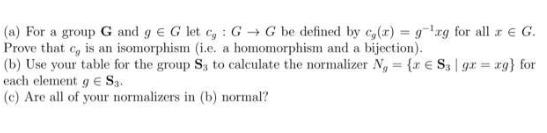
(a) For a group G and g E G let c :

(a) For a group G and g E G let c : GG be defined by ca(r) =gg for all x G. Prove that c, is an isomorphism (i.e. a homomorphism and a bijection). (b) Use your table for the group S, to calculate the normalizer Ng = { S3 | gr=xg} for each element g E Sa (c) Are all of your normalizers in (b) normal?

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The market value balance sheet for Sci-Fi Crimes Manufacturing is shown here. Sci-Fi Crimes has declared a 20 percent stock dividend. The stock goes ex dividend tomorrow (the chronology for a stock...

In this question assume that p and q are atomic formulae. (a) Compare and contrast path formulae and state formulae in temporal logic. [4 marks] (b) Describe and contrast the meanings of F(G p) and...

ttth Suppose that the sequence of bags {Bn | n N} is recursively enumerated by the computable function e(n, x) = fn(x), [7 marks] Hence prove that the set of all recursive bags cannot be recursively...

answer all questions promptly What is the maximum segment length of a 100Base-FX netdwork,Thelast character('X', etc) refers to the line code method used. Line code is a pattern of voltage, current...

This question involves the use of AGGREGATE linear PYTHOIN regression on the Auto data set. (a) Perform a simple linear regression with mpg as the response and horsepower as the predictor. Describe...

DETAILS What is the maximum segment length of a 100Base-FX netdwork, The last character ('X', etc) refers to the line code method used. Line code is a patdtern of voltage, current or photons used to...

$$explain clearly... 2.4 Tangent Lines and Implicit Differentiation 1. At what point on the curve y = sinh r does the tangent line have a slope of 1? 2. Find the point(s) on the graph y = a where the...

Hello, I have an abstract algebra question. I need your help. Thank you so much. *2. (6 points) Let N and H be subgroups of a group C. By Q1(a) on Problem Sheet 1, N 0 H is a subgroup of G, and hence...

answer both parts please 2. Let G be a group. For any 0,? E G, let [6,1'] : error17']. (This is called the commutator of or and 1*.) Let [0,0] denote the group generated by all commutators [U,T] as...

2. Show that if H and K are subgroups of an abelian group G, then {hkh E H, k E K } is a subgroup of G. 3. Prove that if G is an abelian group with identity e, then all elements x in G satisfying x2...

Find A in terms of B if: 2A - B = 5(A + 2B)

The following data represent the concentration of total suspension particulates (TSS) for Al-Hilla river with unit of (mg/1): 640 860 734 510 647 508 710 555 781 500 999 687 500 932 888 601 931 741...

Differentiate the function. g ( x ) = 5 4 x 2 6 x + 1 1 g ( x ) =

What do you think would be the Cobb-Douglas single best prescription for developing countries to catch up with advanced countries?

if U 1 , U 2 , U 3 , and U 4 are vectors in R 7 and U 2 = 0, then the set S= [U 1 ,U 2 ,U 3 ,U 4 ] is linearly dependet . True False

Electric field due to antenna in free space is Es = 10/r *sin * (e^(-j3r)) a V/m. Find (a) Hs (b) average power crossing the surface r=2, 0

U1 U2 A3 Ue T. Ac 1 2 3 15

You have just bought a used track-type tractor to add to your production fleet The initial capitalized value of the tractor is S110.000. The estimated service life remaining on the tractor is 10.000...

6 Theory of Machines 5. A shaft carries five masses A, B, C, D and E which revolve at the same radius in planes which are equidistant from one another. The magnitude of the masses in planes A, C and...

Suppose we have stored n keys in a hash table of size m, with collisions resolved by chaining, and that we know the length of each chain, including the length L of the longest chain. Describe a...

Suppose that the vertices for an instance of the traveling-salesman problem are points in the plane and that the cost c (u, ) is the euclidean distance between points u and . Show that an optimal...

Professor Karan measures her deterministic multi-threaded algorithm on 4, 10, and 64 processors of an ideal parallel computer using a greedy scheduler. She claims that the three runs yielded T 4 = 80...

=+3. According to Rogers, what three qualities do individuals need to receive in a relationship in order to connect with their feelings and desires?

=+2. What name did Maslow give to the motivation to develop to ones full human potential?

=+3. States differ in terms of their laws regarding gay and lesbian adoption rights and employment and housing protections. Research your own states legal policies toward the rights of gay men and