A "greedy" algorithm is one that, in the face of too many possible choices to choose the best from, pursues a good solution to the problem one step at a time. At each step, a greedy algorithm makes a choice that seems best at that moment, without considering that this choice may make future steps less fruitful, achieving a final solution that may be good enough but not the best among all possible solutions. For example, assume you want to drive from city A to city B through highways that require payment of tolls with coins, and you dont have much cash with you (much less in coins!). You would like to take the route from A to B that minimizes the overall spending on toll fees. You could look at all routes you could take, how much each road in a route charges, and spend some time finding the overall best solution. If the route involves many possibilities, this can take quite a while. The greedy solution is simpler: at each time you have to choose a new highway, you select the one that charges less for the toll. It may be that you do very well with this strategy, but there is no guarantee it will work out well enough. It could be that you end up taking cheap roads that lead you to a very expensive area, where all following alternatives cost a lot, revealing that your greedy choices led to an expensive overall solution.

For the terrain maps that we are dealing with, we can envision a "walk" as starting in some cell at the left-most edge of the map (column 0) and proceeding forward by taking a "step" into one of the 3 adjacent cells in the next column over (column 1). (Well, if you are the top or bottom row of the region, you only have 2 possibilities, but unless your region is very small, most of the time you have 3 choices.) Note that steps can take you uphill or downhill. If you want to move from one side of the region to the other (lets say, from the west to the east edge of the region), there are way too many possible paths to consider: if n steps are necessary to traverse the region, the number of possible paths is close to 3n. For the maps you handled in Homework 4, for example the one with 480 rows and 480 columns, you have 480 possible rows to start your walk and you need 479 steps to get to the other side, resulting in approximately 480 * 3479 possible paths. This is a huge number, so considering each possible path when searching for a good solution (e.g., one that minimizes uphill movement) is a bad idea.

The diagrams illustrate a few rules for choosing where to move to at each step. In the case of a tie with the straight-forward position (east direction), you should always choose to go straight forward. In the case of a tie between the two non-forward locations, you should always choose the southeast movement (the one on bottom).

Requirements

You implemented (as required by Part 1) code that read the topographical data from an input file, manipulated it to identify the appropriate gray scale value to display it, and generated an output file following a simple format to represent images.

For Homework Part 2, you need to compute all paths (from the west to the east side of the terrain) that follow the policy of path of least resistance. As you call the function creating each path, you will need to keep track of which is the shortest path. Then you will go back and call the function for that path again, painting it a different color. Well expect the output file generated by your program will produce a visualization similar to the ones depicted below. These are based on the sample input files from Part 1.

Program Flow

Your program starts by executing the first 3 steps from Part 1:

Read the data into a 2D vector

Find min and max elevation to correspond to darkest and brightest color, respectively

Compute the shade of gray for each cell in the map

In Part 1, you completed the assignment by producing the output file (image file in the PPM format) and used a tool to look at the visualization of your output.

For Part 2, your new steps are:

Step 4: Compute a greedy path

Write a function that calculates distance of the path created for a starting row and colors that path a particular color.

For a row, you color the cell you are at using the RGB color value passed in as three int parameters to the function, and compute your next position (following the specified movement rules) and color it, until you get to the last column. To choose the direction to move at each step, you look at the elevation data (that you read from a file) and compute the difference. Remember that you can be going downhill or uphill, therefore when you compute your vertical movement/distance, notice that it may end up negative, and you will need to compare the absolute value of vertical differences. As you color the path, you also have to compute the total distance. This is used to identify the best among all the greedy paths. You will need to return this distance at the end of the function.

The function will compute the greedy path starting at the given row and color it with the provided RGB color value, returning the total vertical movement. Every step you take should follow the greedy choice strategy we described (including what to do when there are ties.) As you move through the path, keep a running total of the total elevation change that would be 'experienced' by a person walking this path. Since we consider an elevation change the absolute value (i.e. going 'uphill' 10 meters is the same amount of change as going 'downhill' 10 meters), this running total will be non-decreasing and may end up being a pretty large positive number. The function should return this running total, so that you can compare it with other totals.

Greedy Function Requirements

The function declaration and definition should be placed in separate header and source files named functions.h (or functions.hpp) and functions.cpp. You may place other functions there as well.

The function signature/prototype is:

int colorPath(const vector>& heightMap, vector>& r, vector>& g, vector>& b, int color_r, int color_g, int color_b, int start_row);

1st parameter is the 2d vector of elevation data

2nd parameter is 2d vector of red values for an RGB color for the corresponding row,col location in the elevation data

3rd parameter is 2d vector of green values for an RGB color for the corresponding row,col location in the elevation data

4th parameter is 2d vector of blue values for an RGB color for the corresponding row,col location in the elevation data

5th parameter is the red value for the RGB path color. This color will replace the grey color of corresponding row,col locations of the path

6th parameter is the green value for the RGB path color. This color will replace the grey color of corresponding row,col locations of the path

7th parameter is the blue value for the RGB path color. This color will replace the grey color of corresponding row,col locations of the path

8th parameter is index of the starting row to begin procedure on.

Returns the distance of the path. This is the sum of changes in elevation from one column to the next.

Step 5: Call Function

Call the greedy algorithm function ( colorPath()) for each row (a loop works well). The greedy path should start on the west edge of the row (i.e. index 0) and color in red [RGB(252,25,63)] the corresponding cells in your output RGB data. While executing the loop, keep track of which row has the shortest path. If more than one path is shortest, then use the one with the lowest index.

Step 6: Paint shortest path

Call the function again for the row with the shortest path using this green [RGB(31,253,13)] for the color.

Then you conclude by carrying out steps you already implemented in Part 1:

Produce the output file in the specified format (PPM) (You already did this in Part 1)

Use an online free tool to convert your PPM file into a JPG file

Below is the code I already have

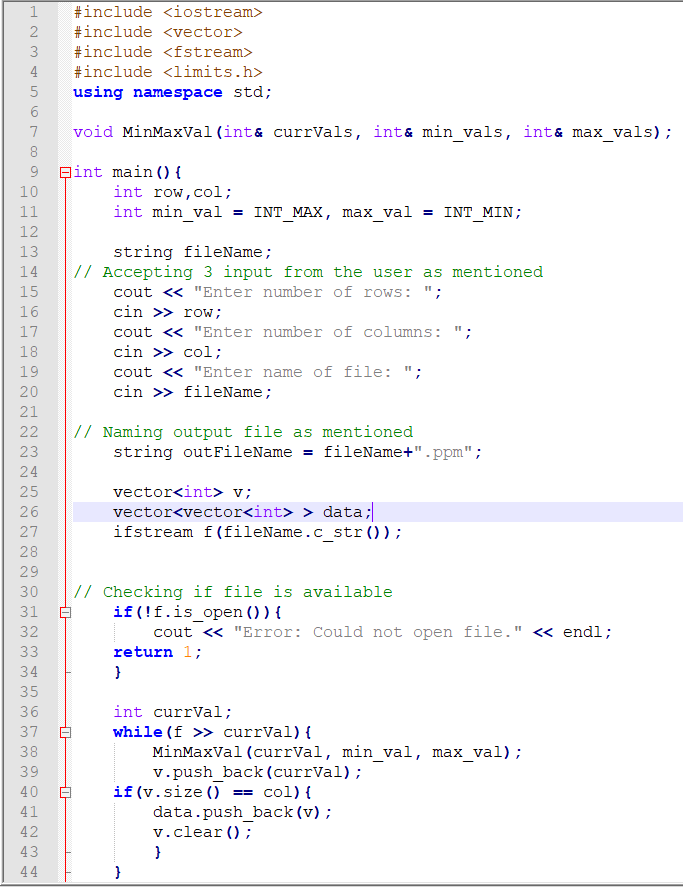
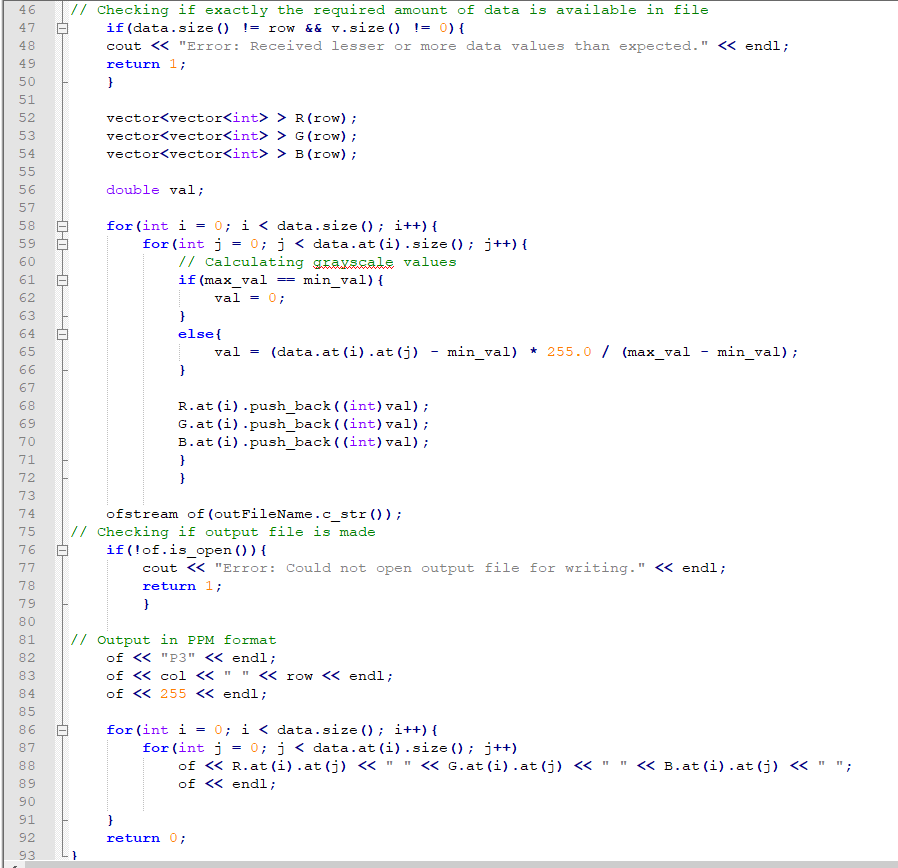
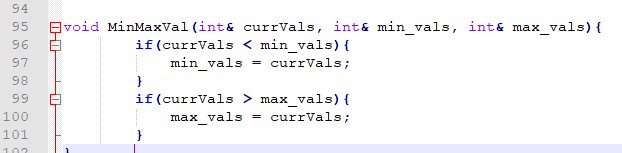
#include #include #include #include 2 3 5 using namespace std; 7 void MinMaxVal (int& currVals, int& min vals, int& max vals); 9 Bint main) 10 int row,col; int min val = INT MAX , max val = INT MIN ; 12 13 14 // Accepting 3 input from the user as mentioned 15 16 17 18 19 20 21 22 I/ Naming output file as mentioned 23 24 25 26 27 28 29 30 // Checking if file is available 31 32 string fileName; cout > row: cout > fileName; string outFileName = fileName+".ppn". vector v; vector > data; ifstream f(fileName.c str (; if (!f.is_open )) i cout > currVal) ( MinMaxVal (currVal, min val, max val); v.push back (currVal); if (v.size () -col) data.push back (v); v.clear(); 43 #include #include #include #include 2 3 5 using namespace std; 7 void MinMaxVal (int& currVals, int& min vals, int& max vals); 9 Bint main) 10 int row,col; int min val = INT MAX , max val = INT MIN ; 12 13 14 // Accepting 3 input from the user as mentioned 15 16 17 18 19 20 21 22 I/ Naming output file as mentioned 23 24 25 26 27 28 29 30 // Checking if file is available 31 32 string fileName; cout > row: cout > fileName; string outFileName = fileName+".ppn". vector v; vector > data; ifstream f(fileName.c str (; if (!f.is_open )) i cout > currVal) ( MinMaxVal (currVal, min val, max val); v.push back (currVal); if (v.size () -col) data.push back (v); v.clear(); 43