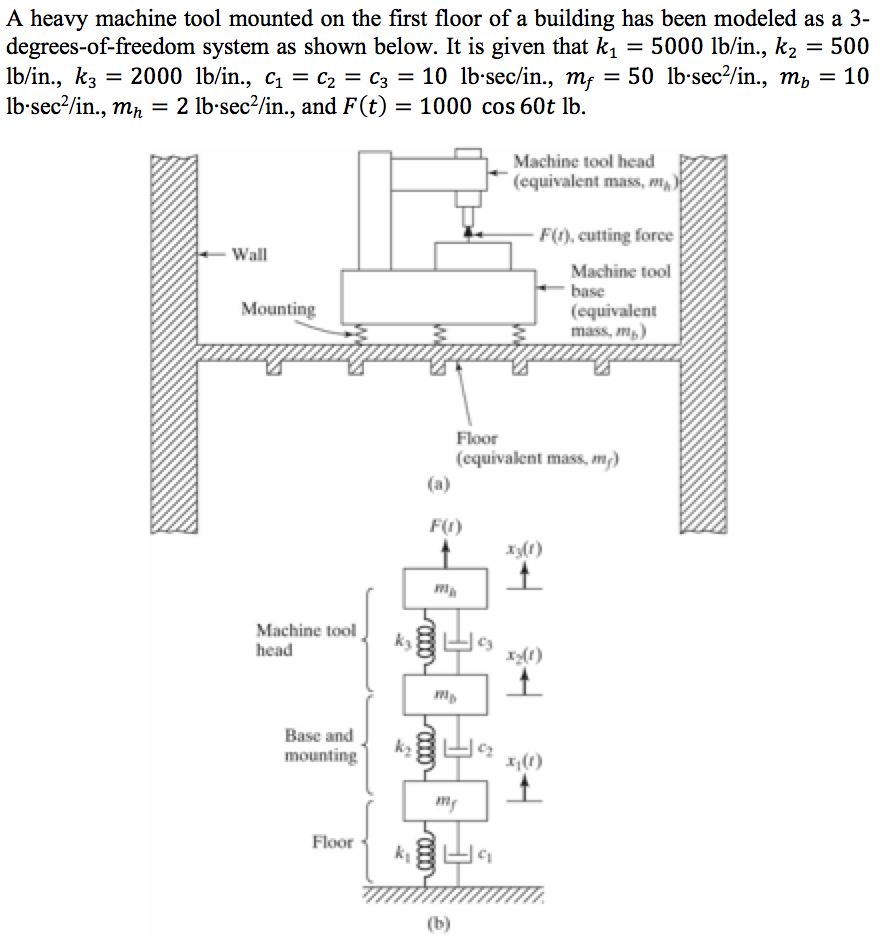
A heavy machine tool mounted on the first floor of a building has been modeled as a 3- degrees-of-freedom system as shown below. It is given that k = 5000 lb/in., k = 500 lb/in., k3 = 2000 lb/in., C = C = C3 = 10 lb-sec/in., mf = 50 lb-sec/in., m = 10 lb-sec/in., m = 2 lb-sec/in., and F(t) = 1000 cos 60t lb. - Wall Mounting Machine tool head Base and mounting Floor (a) F(1) 0000 0000 my Machine tool head (equivalent mass, m) Floor (equivalent mass, my) 0 F(r), cutting force Machine tool base xy(1) 1 x(1) t (equivalent mass, m.) x (1) 1. Derive its forced vibration EOM using Lagrange's equation; 2. Find the steady-state vibration of the system using the mechanical impedance method described in Section 5.6 of Rao's textbook; 3. If the maximum response of the machine tool head (x3) has to be reduced by 25%, how should the stiffness of the mounting (k) be changed? Is there a better way to achieve this goal? Provide details; 4. Verify the steady-state motions of the machine tool through MATLAB simulation.