Answered step by step
Verified Expert Solution
Question
1 Approved Answer
A lock requires a sequence of 5 letters of the alphabet. How many different possible combinations can be created? 26^5 11,881,376 26 x 25
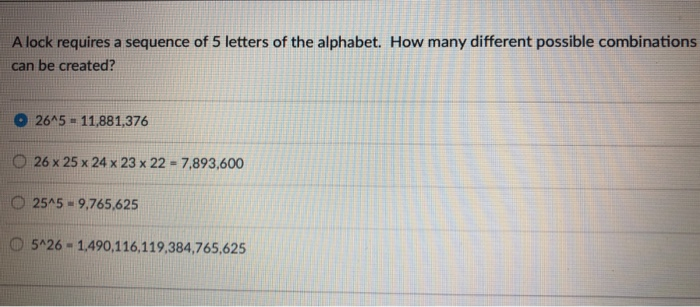
A lock requires a sequence of 5 letters of the alphabet. How many different possible combinations can be created? 26^5 11,881,376 26 x 25 x 24 x 23 x 22= 7,893,600 O25^5-9,765,625 5^261,490,116,119,384,765,625
Step by Step Solution
★★★★★
3.54 Rating (151 Votes )
There are 3 Steps involved in it
Step: 1
In general there are 26 alphabets So for 5 letter lock we ...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2
Step: 3
Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started
Basic Business Statistics Concepts And Applications
Authors: Mark L. Berenson, David M. Levine, Timothy C. Krehbiel
12th Edition
132168383, 978-0132168380
