a) Matrix class: (6 pts) (see class test program pages 4-5) We are asked to design a Class called Matrix which allows to create, display and transpose integer-valued square matrices. The class contains (see UML  figure 1) Private data: oh nligs, o ncols, o matrix: two-dimensional array of integers representing the matrix. Three builders: - The first, without arguments, creates a Matrix type object with dimensions 3 rows by 3 columns with random integers between 0 and 100 inclusive. 2 - The second initializes a Matrix-type object with dimensions of nligs rows by ncols columns with random integers between 0 and 100 inclusive. - The third constructs a Matrix-type object from a two-dimensional array of whole numbers. Public methods: - Accessors for private data: nligs, ncols - A method getValueAt(int i, int j) which returns the value of the element (i,j) of the matrix. - A method setValueAt(int i, int j, int newValue) which modifies the value of the element (i,j) of the matrix. - A method transpose() which performs the transposition of the matrix on which was made the call. - A toString() method that replaces (override) the toString method in the Object class and prints the contents of the matrix.

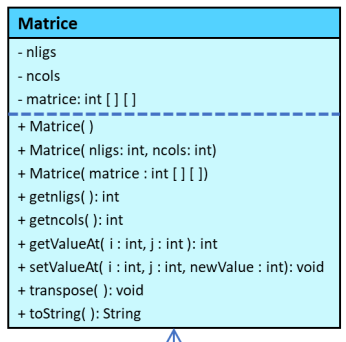
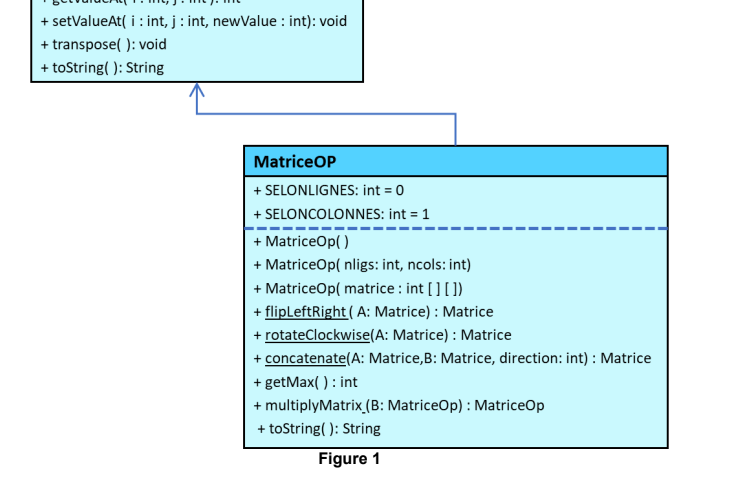
b) MatriceOp class (see class test program on pages 4-5) We are now asked to design a class called MatrixOp extension of the class Matrix to perform some basic matrix operations with objects of types Matrix and MatrixOp. The class contains (see UML  figure 1): (5 pts) Public constants: o ALONGLINES: integer constant which equals 0. o ACCORDING: integer constant which equals 1. Three constructors: (equivalent to those of the Matrix class) - The first, without arguments, creates an object of type OpMatrix of dimensions 3 rows by 3 columns with random integers between 0 and 100 inclusive. - The second initializes an object of type MatriceOp of dimensions nligs lines by ncols columns with random integers between 0 and 100 inclusive. - The third constructs an object of type OpMatrix from a two-dimensional array of whole numbers.

 Three public static methods: (you must implement one of the three of your choice) - A static method flipLeftRight(Matrix A) which returns a Matrix type object which is the permutation of the matrix A around its vertical center (see execution example below) below). - A static method rotateClockwise(Matrix A) which returns a Matrix type object which is the rotation of the matrix A clockwise (rotation 90 degrees). - A static method concatenate(Matrix A, Matrix B, int direction) which returns a Matrix type object which is the concatenation of matrices A and B as follows: a) If direction=Matrix.ALONGLINES, the concatenation is done in the form [A B] b) If direction=Matrix.ACCORDINGCOLUMNS, the concatenation is done in the form [ AT B ] In a) the result matrix has a number of rows equal to the greatest number of rows between A and B. Missing row elements will be filled with zero in the result matrix. In b) the result matrix has a number of columns equal to the largest number of columns between A and B. The missing column elements will be filled by zero in matrix results. Two public instance methods: (you must implement one of the two of your choice) - A method getMax( ) which returns the maximum element in the Matrix on which was made the call.. - A method multiplyMatrix( MatriceOp B ) which returns an object of type MatriceOp which is the product of the Matrix on which the call was made with Matrix B. A public toString() method: - A toString() method that replaces (override) the toString method in the Matrix class and prints the content of the matrix with its maximum. 4 An example of a test program of these two classes is given below, the result is found on the next page, Figure 2.

\begin{tabular}{|l|} \hline Matrice \\ \hline - nligs \\ - ncols \\ - matrice: int [ ] [ ] \\ + Matrice( nligs: int, ncols: int) \\ + Matrice( matrice : int [ ] [ ]) \\ + getnligs( ): int \\ + getncols( ): int \\ + getValueAt( i : int, j : int ): int \\ + setValueAt( i : int, j : int, newValue : int): void \\ + transpose( ): void \\ + toString( ): String \\ \hline \end{tabular} +setValueAt(i:int,j:int,newValue:int):void+transpose():void+toString():String