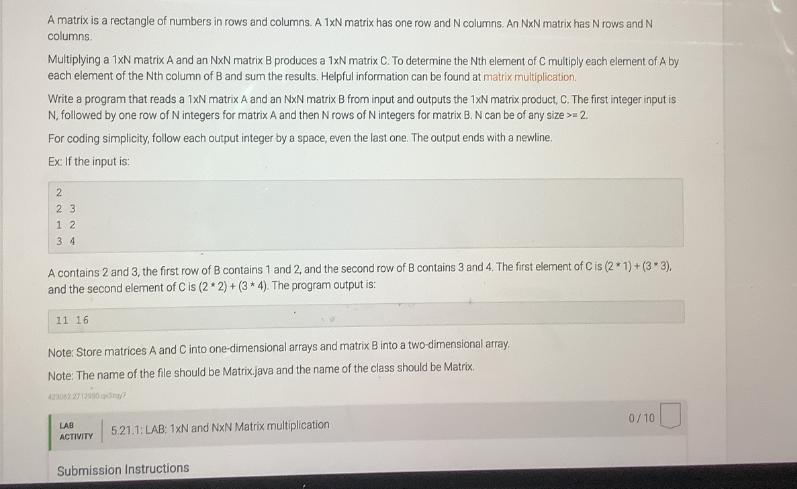
A matrix is a rectangle of numbers in rows and columns. A 1xN matrix has one row and N columns. An NxN matrix has N rows and N columns. Multiplying a 1xN matrix A and an NxN matrix B produces a 1xN matrix C. To determine the Nth element of C multiply each element of A by each element of the Nth column of B and sum the results. Helpful information can be found at matrix multiplication. Write a program that reads a 1xN matrix A and an NXN matrix B from input and outputs the 1xN matrix product, C. The first integer input is N, followed by one row of N integers for matrix A and then N rows of N integers for matrix B. N can be of any size >= 2. For coding simplicity, follow each output integer by a space, even the last one. The output ends with a newline. Ex: If the input is: 2 23 12 3.4 A contains 2 and 3, the first row of B contains 1 and 2, and the second row of B contains 3 and 4. The first element of C is (21) + (3*3), and the second element of C is (2*2)+(3 * 4). The program output is: 11 16 Note: Store matrices A and C into one-dimensional arrays and matrix B into a two-dimensional array. Note: The name of the file should be Matrix.java and the name of the class should be Matrix. 42306227129907 LAB ACTIVITY 5.21.1: LAB: 1xN and NxN Matrix multiplication Submission Instructions 0/10