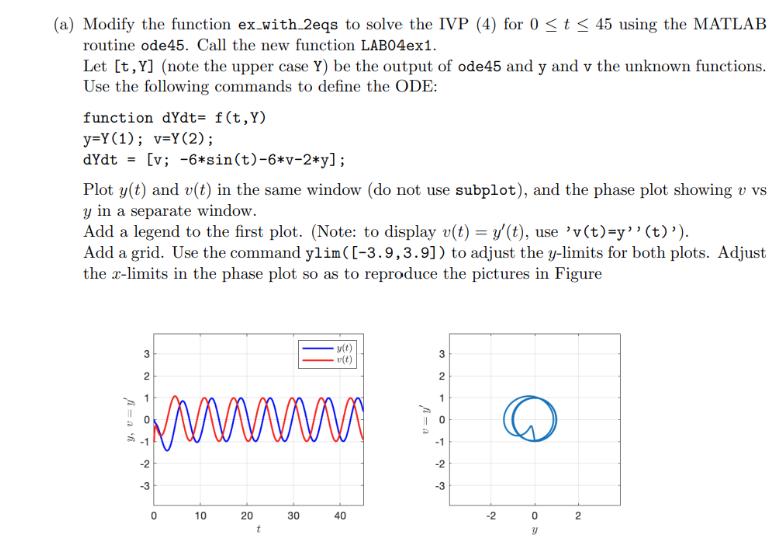
(a) Modify the function ex_with_2eqs to solve the IVP (4) for 0 t 45 using the MATLAB routine ode45. Call the new function LAB04ex1. Let [t,Y] (note the upper case Y) be the output of ode45 and y and v the unknown functions. Use the following commands to define the ODE: function dYdt= f(t,Y) y=Y (1); v=Y (2); dYdt = [v; -6* sin(t)-6*v-2*y]; Plot y(t) and v(t) in the same window (do not use subplot), and the phase plot showing v vs y in a separate window. Add a legend to the first plot. (Note: to display v(t) = y(t), use 'v(t)=y'' (t)'). Add a grid. Use the command ylim ([-3.9,3.9]) to adjust the y-limits for both plots. Adjust the x-limits in the phase plot so as to reproduce the pictures in Figure 3 2 1 0 -1 www -2 -3 0 10 20 t y(t) v(t) 30 40 A-a 3 2 1 0 -1 -2 -3 -2 0 Y 2 Figure Time series y = y(t) and v=v(t) = y'(t) (left), and phase plot v = y' vs. y for (4). (b) By reading the matrix Y and the vector t, find (approximately) the last three values of t in the interval 0 t 45 at which y reaches a local maximum. Note that, because the M-file LAB04ex1.m is a function file, all the variables are local and thus not available in the Command Window. To read the matrix Y and the vector t, you need to modify the M-file by adding the line [t, Y(:,1), Y(:,2)]. Do not include the whole output in your lab write-up. Include only the values necessary to answer the question, i.e. just the rows of [t, y, v] with local y-maxima and the adjacent rows. To quickly locate the desired rows, recall that the local maxima of a differentiable function appear where its derivative changes sign from positive to negative. (Note: Due to numerical approximations and the fact that the numerical solution is not necessarily computed at the exact t-values where the maxima occur, you should not expect v(= y) to be exactly 0 at local maxima, but only close to 0). (c) What seems to be the long term behavior of y? (d) Modify the initial conditions to y(0) = 1.1, v(0) = -1.2 and run the file LAB04ex1.m with the modified initial conditions. Based on the new graphs, determine whether the long term behavior of the solution changes. Explain. Include the pictures with the modified initial conditions to support your answer.