Answered step by step
Verified Expert Solution
Question
1 Approved Answer
A movie has start times of 7:00, 7:25, and 7:50 p.m. You arrive randomly at the theater between 7:00 and 7:50 p.m. Let x be

- A movie has start times of 7:00, 7:25, and 7:50 p.m. You arrive randomly at the theater between 7:00 and 7:50 p.m. Let x be the number of minutes after 7:00 that you arrive at the theater. (a) What is the distribution of x? f(x) = ?, for _____? x ?_______? (b) What is the probability that you wait less than 20 minutes until a movie starts? (c) What is the probability that you wait more than 20 minutes until a movie starts?
- An oil exploration company purchases drill bits that have a life span that is approximately normally distributed with a mean equal to 87 hours and a standard deviation equal to 12 hours. (a) What proportion of the company's drill bits will fail before 78 hours of use? (b) What proportion will last at least 78 hours? (c) What proportion will have to be replaced after more than 96 hours of use?
- Most users of automatic garage door openers activate their openers at distances that are normally distributed with a mean of 30 feet and a standard deviation of 11 feet. To minimize interference with other remote-controlled devices, the manufacturer is required to limit the operating distance to 53 feet. What percentage of the time will users attempt to operate the opener outside its operating limit? (Round your answer to two decimal places.)
- The length of time required to run a 5000-mile check and to service an automobile has a mean equal to 1.2 hours and a standard deviation of 0.7 hours. What is the probability that the next customer requiring a 5000-mile check and service will have to wait longer than 1.6 hours for the service to be completed? (Round your answer to four decimal places.)
- Psychologists believe that excessive eating may be associated with emotional states (being upset or bored) and environmental cues (watching television, reading, and so on). To test this theory, suppose you randomly selected 64 persons and matched them by weight and gender in pairs. For a period of 2 weeks, one of each pair spends evenings reading novels of interest to him or her, while the other spends each evening watching television. You record x = 20, the number of pairs for which the television watchers' calorie intake exceeded the intake of the readers. If there is no difference in the effects of television and reading on calorie intake, the probability p that the calorie intake of one member of a pair exceeds that of the other member is 0.5. Do these data provide sufficient evidence to indicate a difference between the effects of television watching and reading on calorie intake? (HINT: Calculate the z-score for the observed value, x = 20. Round your answer for the z-score to two decimal places.) The z-score is , which is two standard deviations of the mean. This is a occurrence. Hence, we would have to believe that there is a difference between calorie intake for television watchers versus readers.
- Suppose that the IRS assigns auditing rates per state by randomly selecting 50 auditing percentages from a normal distribution with a mean equal to 1.55% and a standard deviation of 0.45%. (a) What is the probability that a particular state would have more than 2% of its tax returns audited? (Round your answer to four decimal places.) (b) What is the expected value of x, the number of states that will have more than 2% of their income tax returns audited? (Round your answer to three decimal places.) (c) Is it likely that as many as 15 of the 50 states will have more than 2% of their income tax returns audited? Because x = 15 has a z-score of at least 2, it is likely that as many as 15 of the 50 states will have more than 2% of their income tax returns audited. Because x = 15 has a z-score of at least 2, it is unlikely that as many as 15 of the 50 states will have more than 2% of their income tax returns audited.Because x = 15 has a z-score less than 2, it is unlikely that as many as 15 of the 50 states will have more than 2% of their income tax returns audited. Because x = 15 has a z-score less than 2, it is likely that as many as 15 of the 50 states will have more than 2% of their income tax returns audited.
- Allen Shoemaker derived a distribution of human body temperatures, which has a distinct mound-shape.? Suppose we assume that the temperatures of healthy humans is approximately normal with a mean of 98.6 degrees and a standard deviation of 0.8 degrees. (a) If a healthy person is selected at random, what is the probability that the person has a temperature above 99.4 degrees? (Round your answer to four decimal places.) (b) What is the 90th percentile for the body temperatures (in ) of healthy humans?
- A study indicates that if eight people occupy the elevator, the probability distribution of the total weight of the eight people is approximately normally distributed with a mean equal to 1,250 pounds and a standard deviation of 96 pounds. What is the probability that the total weight of eight people exceeds 1,400 pounds? What is the probability that the total weight of eight people exceeds 1,500 pounds?
- The admissions office of a small college is asked to accept deposits from a number of qualified prospective freshmen so that, with probability about 0.95, the size of the freshman class will be less than or equal to 1,900. Suppose the applicants constitute a random sample from a population of applicants, 80% of whom would actually enter the freshman class if accepted. (Use the normal approximation.) (a) How many deposits should the admissions counselor accept? (Round your answer up to the nearest integer.) deposits (b) If applicants in the number determined in part (a) are accepted, what is the probability that the freshman class size will be less than 1,860? (Use the exact number of accepted applicants you found in part (a). Round your answer to four decimal places.)
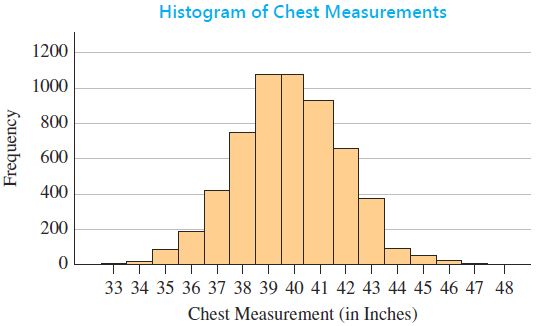
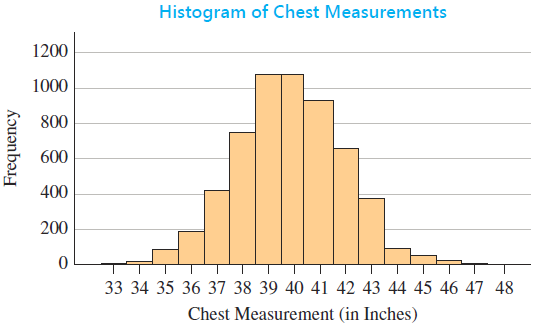
- The chest measurements for 5,738 Scottish militiamen in the early 19th century are given below. Chest sizes are measured in inches, and each observation reports the number of soldiers with that chest size. Notice the approximate normality of the histogram of the 5,738 chest measurements. A histogram labeled "Histogram of chest Measurements" has a horizontal axis labeled "Chest Measurement (in Inches)" with values from 33 to 48 and a vertical axis labeled "Frequency" with values from 0 to 1,200. The histogram has 16 bars. Each bar is associated with a label and an approximate value as listed below.
- 33: 3
- 34: 18
- 35: 81
- 36: 185
- 37: 420
- 38: 749
- 39: 1,073
- 40: 1,079
- 41: 934
- 42: 658
- 43: 370
- 44: 92
- 45: 50
- 46: 21
- 47: 4
- 48: 1 (a) The mean of this distribution is x = 39.83 and the standard deviation is s = 2.05. What is the 95th percentile of this distribution (in inches) based on a normal curve with ? = 39.83 and ? = 2.05? (b) Find the empirical estimate of the 95th percentile (in inches) and compare with your answer in part (a). (HINT: The 95th percentile will be in position 0.95(n + 1) = 0.95 ? 5,739 = 5,452.05from the left tail of the distribution or in position 5,738 ? 5,452.05 = 285.95from the right tail of the distribution.) (c) Find the 96th percentile of this distribution (in inches) based on a normal curve with ? = 39.83 and ? = 2.05. (Round your answer to three decimal places.) What is the value of the empirical 96th percentile (in inches)? How does it compare with the value assuming normality?

Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


