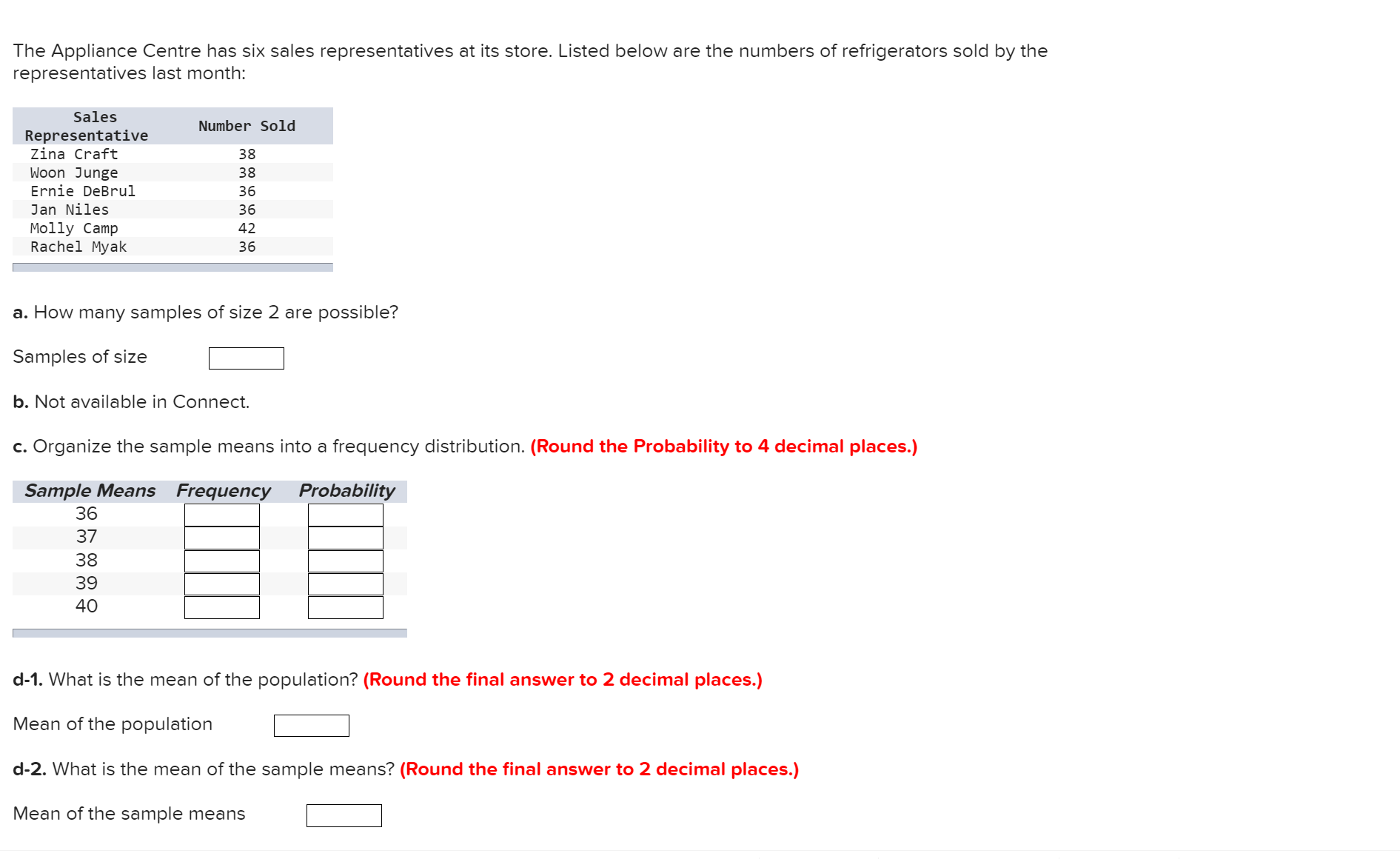
A normal population has a mean of 75 and a standard deviation of 7. You select a sample of 38. Use Appendix Bel for the zvalues. Compute the probability that the sample mean is: (Round the z-values to 2 decimal places and the final answers to 4 decimal places.) a. Less than 74. Probability b. Between 74 and 76, Probability c. Between 76 and 78. Probability d. Greater than 78. Probability It has been estimated that 18% of all university students switch majors within their first two years of starting classes. lfa random sample of 440 thirdyear students is taken at a city university, what is an estimate of the probability that 15% or less had switched majors within their first two years? Use Appendix 31 for the zvalues. (Round the z-value to 2 decimal places and the final answer to 4 decimal places.) Probability The Appliance Centre has six sales representatives at its store. Listed below are the numbers of refrigerators sold by the representatives last month: Sales Representative Number 501d Zina Craft 38 Noon Junge 38 Ernie DeBrul 36 Jan Miles 36 Molly Camp 42 Rachel Myak 36 a. How many samples of size 2 are possible? Samples of size b. Not available in Connect. c. Organize the sample means into a frequency distribution. (Round the Probability to 4 decimal places.) Sample Means Frequency Probability 36 37 38 39 40 d-1. What is the mean of the population? (Round the final answer to 2 decimal places.) Mean of the population d-2. What is the mean of the sample means? (Round the final answer to 2 decimal places.) Mean of the sample means The mean amount of life insurance per household is $129,000. This distribution is positively skewed. The standard deviation of the population is $36,000. Use Appendix EH for the zvalues. a. A random sample of 60 households revealed a mean of $133,000. What is the standard error of the mean? (Round the final answer to 2 decimal places.) Standard error ofthe mean b. Suppose that you selected 133,000 samples of households. What is the expected shape of the distribution of the sample mean? Shape (Click to select) v c. What is the likelihood of selecting a sample with a mean of at least $133,000? (Round the final answer to 4 decimal places.) Probability d. What is the likelihood ofselecting a sample with a mean of more than $121,000? (Round the final answer to 4 decimal places.) Probability e. Find the likelihood of selecting a sample with a mean of more than $121,000 but less than $133,000. (Round the final answer to 4 decimal places.) Probability The Crossett Trucking Company claims that the mean mass of its delivery trucks when they are fully loaded is 2800 kg and the standard deviation is 70 kg. Assume that the population follows the normal distribution. Forty trucks are randomly selected and their masses measured. Within what limits will 95% of the sample means occur? (Round the final answers to the nearest whole number.) Sample means to The average grade in a statistics course has been 77 with a standard deviation of 115. If a random sample of 57 is selected from this population, what is the probability that the average grade is more than 81? Use Agpendix Bil for the zvalues. (Round your z-value to 2 decimal places and the final answer to 4 decimal places.) Probability A population consists of the following five values: 4, 4, 2, 32, 33. a. Not available in Connect. b. By listing all samples of size 3, compute the mean of the distribution of the sample mean and the population mean. Compare the two values. (Round the final answer to the nearest whole number.) Sample means Population mean Both means are (Click to select) v c. Compare the dispersion in the population with that ofthe sample means. Hint Use the range as measure of dispersion. The dispersion of the population is (Click to select) v than that of the sample means. A manufacturing process produces 5% defective items. What is the probability that in a sample of 50 items: a. 9% or more will be defective? (Round the zvalue to 2 decimal places and the final answer to 4 decimal places.) Probability b. less than 3% will be defective? (Round the z-value to 2 decimal places and the final answer to 4 decimal places.) Probability c. more than 9% or less than 3% will be defective? (Round the z-value to 2 decimal places and the final answer to 4 decimal places.) Probability It is estimated that 11% of those taking the quantitative methods portion of the certified public accountant (CPA) examination fail that section. Sixty ve students are taking the examination this Saturday. a-1. How many would you expect to fail? (Round the final answer to 2 decimal places.) Number of students a-2. What is the standard deviation? (Round the final answer to 2 decimal places.) Standard deviation b. What is the probability that exactly three students will fail? (Round the final answer to 4 decimal places.) Probability c. What is the prooability at least three students will fail? (Round the final answer to 4 decimal places.) Probability A population consists of the following five values: 3, 3, 15, 20, and 24. a. Not available in Connect. b. By listing all samples of size 3, compute the mean of the distribution of the sample mean and the population mean. Compare the two values. (Round the final answers to 2 decimal places.) Sample means Population mean Both means are (Click to select) v c. Compare the dispersion in the population with that of the sample means. Hint Use the range as measure of dispersion. The dispersion of the population is (Click to select) v than that of the sample means. A normal population has a mean of 55 and a standard deviation of 21. You select a random sample of 30, Use Appendix 31 for the 2- values. Compute the probability that the sample mean is: (Round the final answers to 4 decimal places.) a. Greater than 58. Probability b. Less than 51. Probability c. Between 51 and 58. Probability