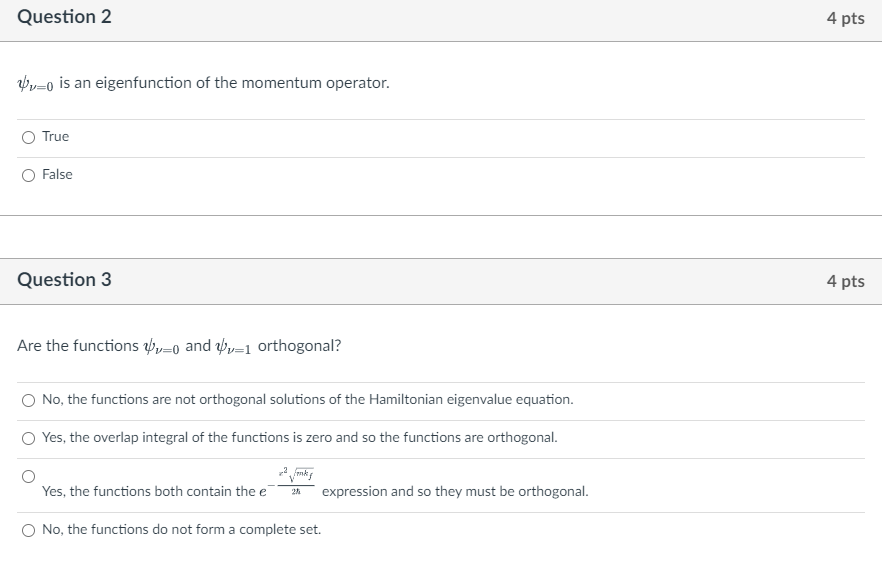
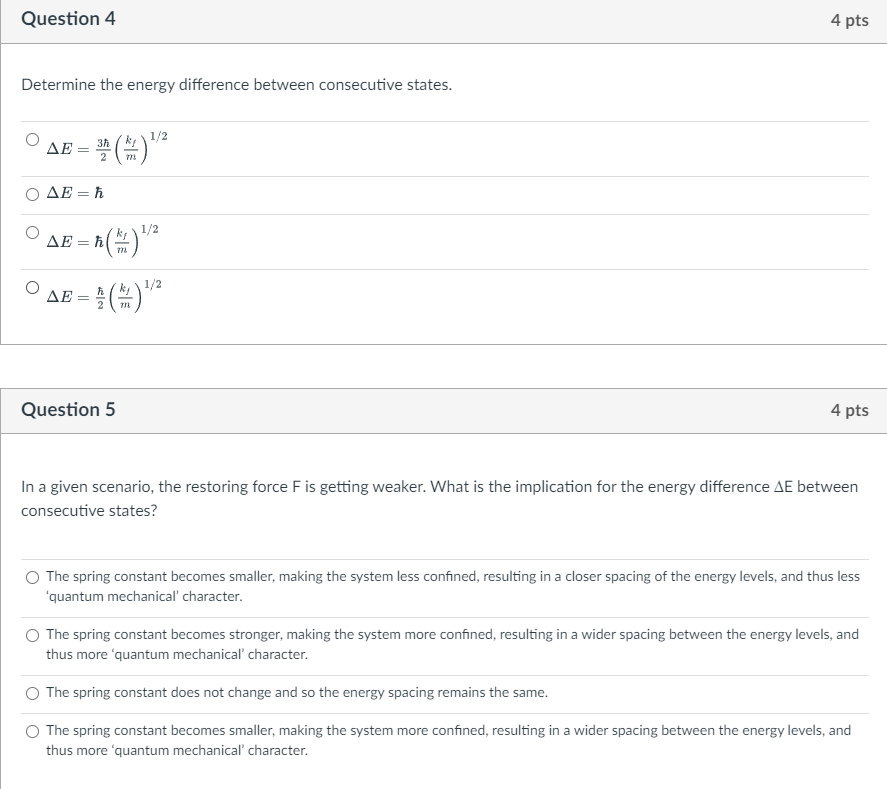
A particle of mass m that is moving along the x-axis is experiencing a restoring force of the form F = -k+x, where kf is the spring constant. The Hamiltonian for this system is given as: = d 2m dx + kfx The first two eigenstates of this system are given as: 2 v=0 = Ae 2 Vv=1 = 2B mkj h 1/4 2 Vmky xe 25 where A and B are constants. Question 1 4 pts Is -1 an eigenfunction of the Hamiltonian? Determine the energy of this state and express your answer in terms of kf W = V m Yes, E = hw No, this function is not an eigenfunction of the Hamiltonian and thus has no eigenvalue. Yes, E = hw O Yes, E = hw Question 2 v=0 is an eigenfunction of the momentum operator. True False Question 3 Are the functions 0 and 1 orthogonal? No, the functions are not orthogonal solutions of the Hamiltonian eigenvalue equation. Yes, the overlap integral of the functions is zero and so the functions are orthogonal. Yes, the functions both contain the e 20 expression and so they must be orthogonal. No, the functions do not form a complete set. 4 pts 4 pts Question 4 Determine the energy difference between consecutive states. = AE=h = 34 (1) 1/2 h(%) 1/2 AE=h 1/2 | AE = }}() "/ Question 5 4 pts 4 pts In a given scenario, the restoring force F is getting weaker. What is the implication for the energy difference AE between consecutive states? The spring constant becomes smaller, making the system less confined, resulting in a closer spacing of the energy levels, and thus less 'quantum mechanical' character. The spring constant becomes stronger, making the system more confined, resulting in a wider spacing between the energy levels, and thus more 'quantum mechanical' character. The spring constant does not change and so the energy spacing remains the same. The spring constant becomes smaller, making the system more confined, resulting in a wider spacing between the energy levels, and thus more 'quantum mechanical' character.