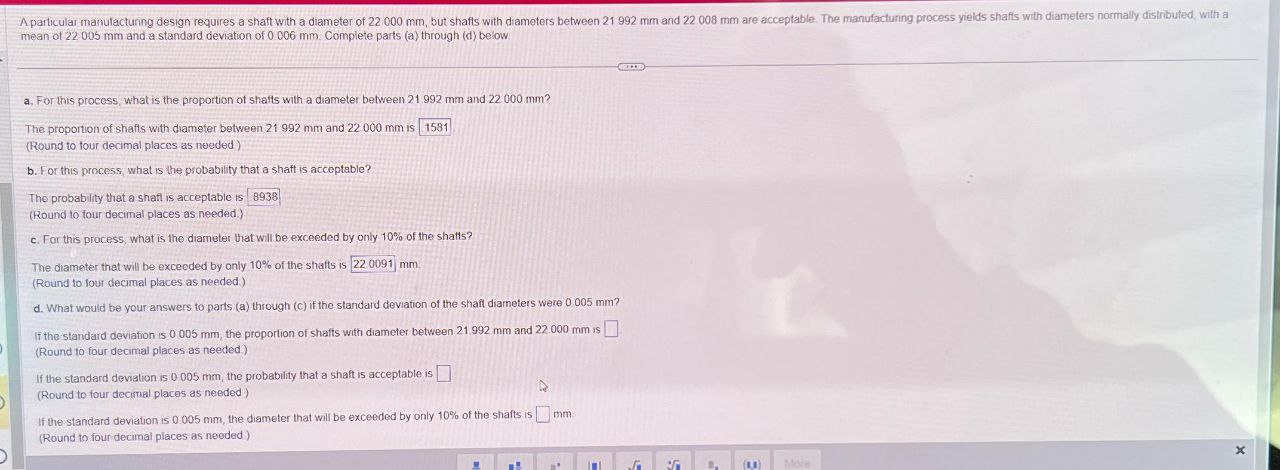
A particular manufacturing design requires a shaft with a diameter of 22 000 mm, but shafts with diameters between 21 992 mm and 22.008 mm are acceptable. The manufacturing process yields shafts with diameters normally distributed, with a mean of 22 005 mm and a standard deviation of 0.006 mm. Complete parts (a) through (d) below a. For this process, what is the proportion of shafts with a diameter between 21 992 mm and 22 000 mm? The proportion of shafts with diameter between 21 992 mm and 22 000 mm is 1581 (Round to four decimal places as needed) b. For this process, what is the probability that a shaft is acceptable? The probability that a shaft is acceptable is 8938 (Round to four decimal places as needed) c. For this process, what is the diameter that will be exceeded by only 10% of the shafts? The diameter that will be exceeded by only 10% of the shafts is 22.0091 mm. (Round to four decimal places as needed.) d. What would be your answers to parts (a) through (c) if the standard deviation of the shaft diameters were 0.005 mm? If the standard deviation is 0 005 mm, the proportion of shafts with diameter between 21.992 mm and 22.000 mm is (Round to four decimal places as needed.) If the standard deviation is 0.005 mm, the probability that a shaft is acceptable is (Round to four decimal places as needed) If the standard deviation is 0.005 mm, the diameter that will be exceeded by only 10% of the shafts is (Round to four decimal places as needed) mm More x