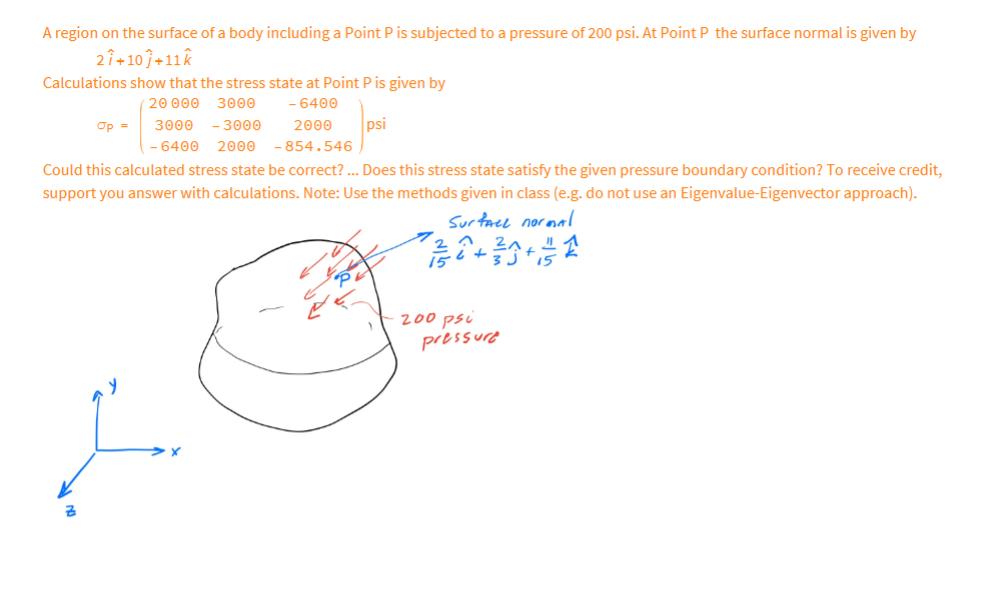
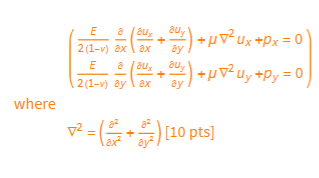
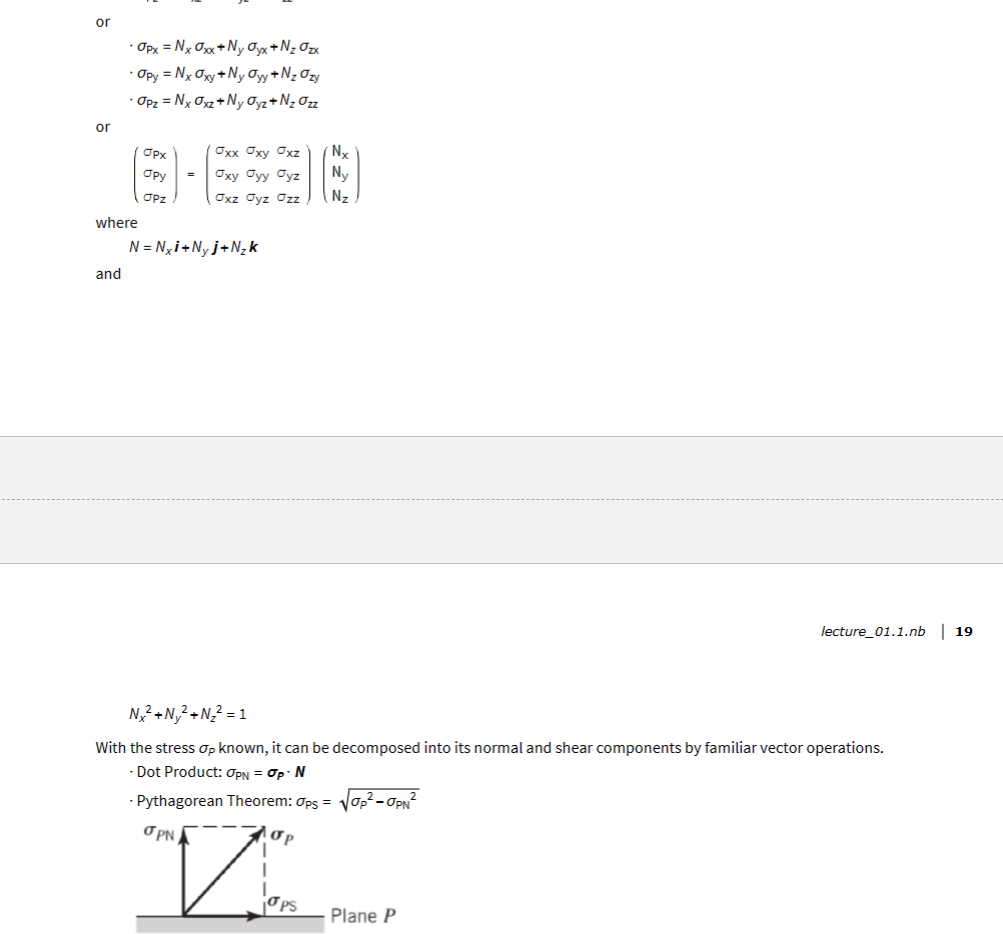
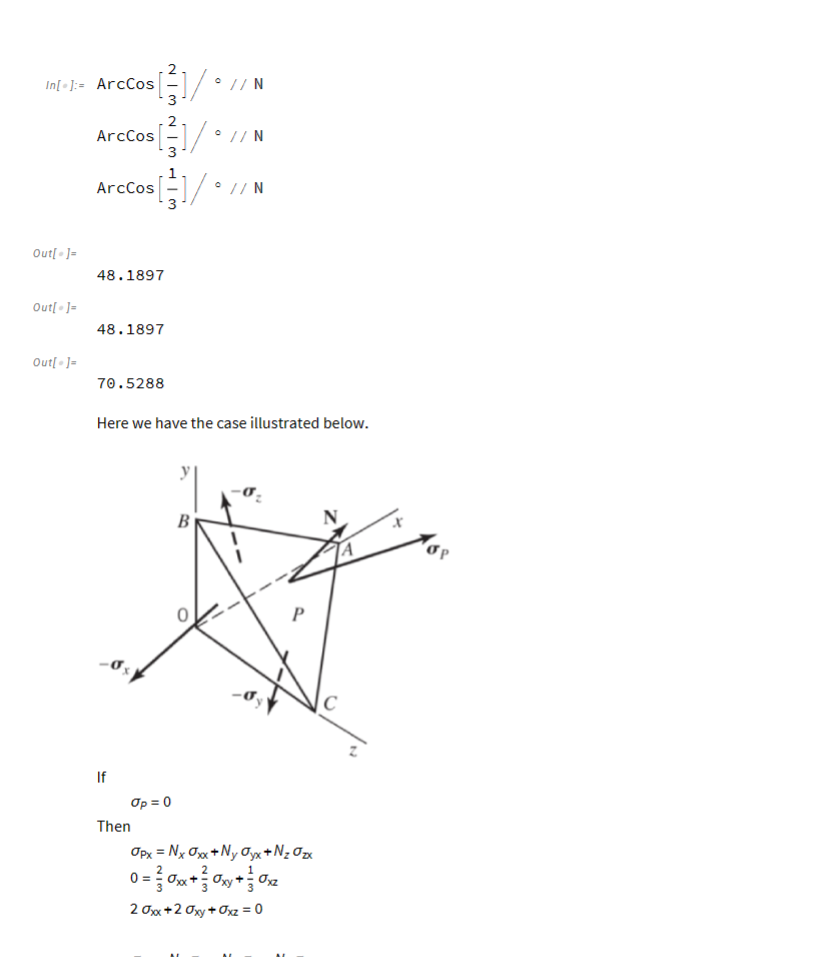
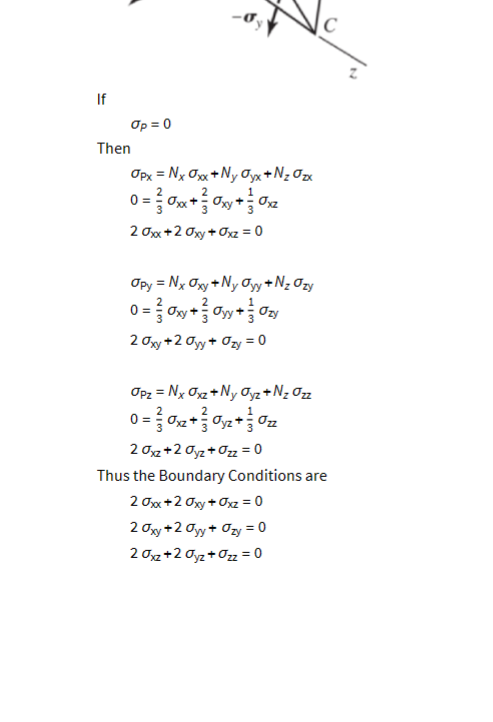
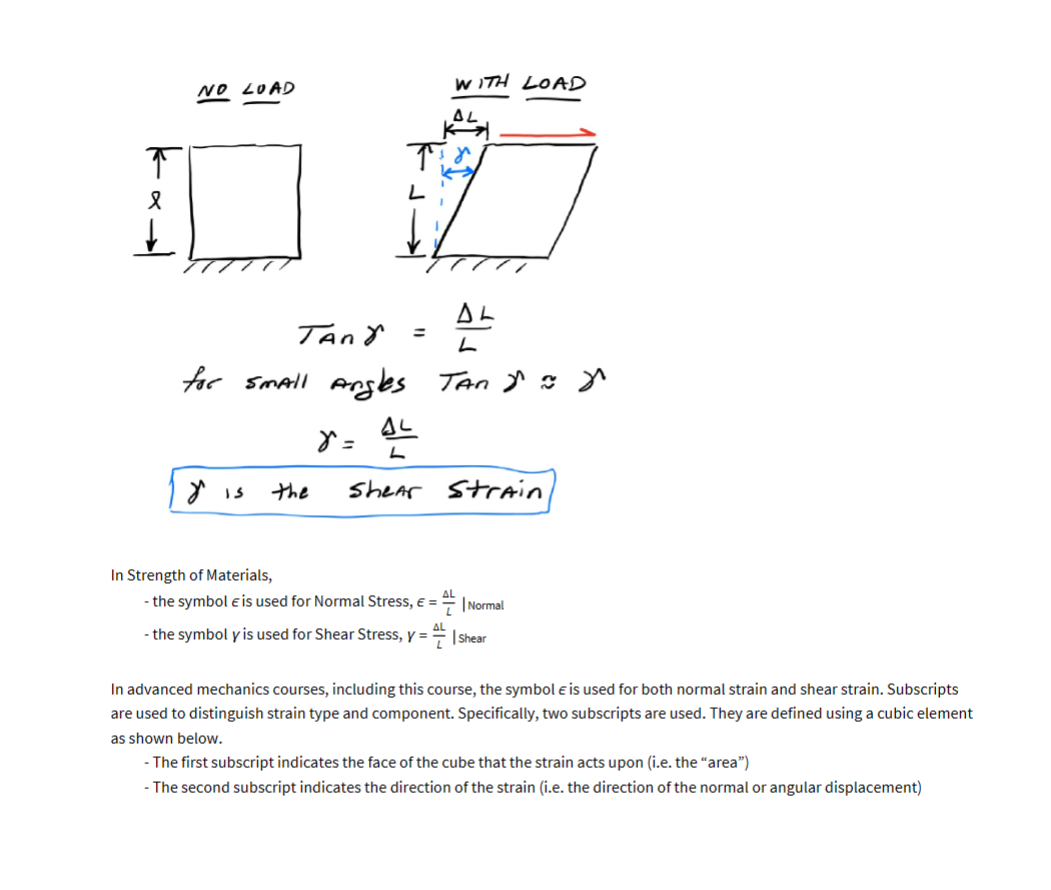
A region on the surface of a body including a Point P is subjected to a pressure of 200 psi. At Point P the surface normal is given by 27+10)+11k Calculations show that the stress state at Point P is given by 3000 - 6400 20 000 3000 - 3000 2000 psi - 6400 2000 -854.546 Could this calculated stress state be correct? ... Does this stress state satisfy the given pressure boundary condition? To receive credit, support you answer with calculations. Note: Use the methods given in class (e.g. do not use an Eigenvalue-Eigenvector approach). Op = L Surface normal 7/2+ 3+2/2 3 J 200 psi pressure Problem 3 Calculate the nine 3D strain values and the six 3D rigid-body rotation values given the displacements below Ux = Cxxz Uy=Cyx y U=Cz-y Problem 4 (a) Does the matrix given below represent a valid strain tensor? Show mathematically why or why not. (0.2 y 0 0 0 -0.2x 0 0 0/ (b) Regardless of your answer to part (a), illustrate the displacement field Ux and Uy by showing a deformed and undeformed square mesh as done in lecture. (c) Comment on the angles between the deformed gridlines. Are the angles consistent with the Shear Strain value given in the matrix of part (a)? Problem 5: Beginning with the 3D Navier Equation, (A+) V divu+vu+p= 0, show that the correct simplified form for Plane Stress Problem 5: Beginning with the 3D Navier Equation, (A+) V divu+uvu+p= 0, show that the correct simplified form for Plane Stress conditions is given by where aux E 2(1-v) ax E a ax ay au aux 0 ( 2 (1-1) oy (4x + 3/4/4) + V uy +Py = ay ax ay auy + 3/) + V Ux+Px = 0) ( 8 v = ( + ) [10 pts] ax In advanced mechanics courses (including this course) the symbol o is used for both normal and shear stress. Subscripts are used to distinguish stress type and component. Specifically, two subscripts are used. They are defined using a cubic element as shown below. - The first subscript indicates the face of the cube that the stress acts upon (i.e. the "area") - The second subscript indicates the direction of the stress (i.e. the direction of the "force component") Thus - Normal stresses have two identical subscripts - Shear stresses have two different subscripts 92 where %2x Jyx Oyy oyz Ozx Ozy Ozz Ox = Oxy Or = oxe Oz=0zy Par The sign of stress is determined by the sign of the face combined with the sign of the direction - Sign of the face: Is the sign of the coordinate axis parallel and in the same direction as the surface normal - Sign of the direction: Is the sign of the coordinate axis parallel and in the same direction as the stress component Face Face Direction As will be proven in a subsequent lecture, a three-dimensional stress state can be written as a symmetric 3x3 matrix Oxx Oxy Oxz Oxx oxy Oxz Oxx Oxy Oyy gyz Oxz Oyz Ozz Stress Acting on an Arbitrary Plane Consider a Point P in a body under load. The stresses at Point P are known with respect to the xyz coordinate system. Oxx 5x7 628 Z (Oxx Oxy Oxz' Op = Oyx ayy yz Ozx Ozy Ozz The above infinitesimal element gives all stresses acting at Point P with respect to planes perpendicular to the coordinate axes. Recall: For visualization, the stress element is shown having finite dimensions. However, since it represents the stress at a point, the point P, it is actually infinitesimally small. However, what if the stresses on a different, non-coordinate, plane at Point P are needed? This could be necessary, for example, to define Boundary Conditions. That is, if Point P was on the surface of the body and we needed to relate the stress state in the body to the stresses acting on the surface. Some common examples are - Stress-free surface - Pressure load - Friction load The needed equations can be developed by considering the tetrahedron below. Note -If the non-coordinate plane is the surface of the body (typical for a Boundary Condition), then the tetrahedron is formed by simply drawing the appropriate lines parallel to the coordinate axes and intersecting the surface -If the non-coordinate plane is interior to the body, then the tetrahedron is formed by bisecting the cubic stress element into two tetrahedrons. Note such a bisection is possible for any non-coordinate plane. The surface-normal unit vector N is defined by its Direction Cosines (the cosines of the angles it forms with the coordinate axes) N=li+mj+nk where /is the Cosine of the angle between N and the x-axis, 8x m is the Cosine of the angle between N and the y-axis, By n is the Cosine of the angle between N and the z-axis, 8 We won't prove it (see ME 523 for that) but it can be shown that AreBosc 1 = Areasc AreBoxc Areasc Areas Area.c m = n = Thus op can be decomposed into its components along the coordinate axes Op = 10px + m Opy+n Opz But . Opx is just the stress in the x-direction which we know from above as 0px = ax = axxi + Oxy j + 0xzk . Similarly we have or Opy = Oy = Oxy+ Oyy j + yzk Opz = 0 = Oxzi+ayz j + Ozzk Substituting gives Op = 10px + m Opy+n Opz =l(xi+xyj+zk)+m(Oxyi+yj+ yzk)+n(zi+yzj+zk) = (10xx+moxy+naxz)i +(/ Oxy+mayy+nOyz)j + (10x+MO+nOz)k This equation Op = (10xx+moxy+noxz)i + (1 Oxy+may+noyz)j + (10x+moyz +nozz) k is known as the Cauchy Stress Equation, The Cauchy Stress Theorem, and Cauchy's Fundamental Theorem. In component form it is Opx = 10xx+mayx +nozx Opy = / Oxy+m ayy + nozy Opz = 1 Oxz+m Oyz +n Ozz or or Opx = Nx Oxx+Ny Oyx +Nz Ozx Opy = Nx Oxy +Ny Oyy + N Ozy Opz = Nx Oxz+Ny Oyz + N Ozz where and Opx Opy OPZ = Oxx Oxy Oxz Nx Ny Oxy Jyy dyz Oxz Oyz Ozz N N=Nxi+Nyj+Nk N+N+N = 1 With the stress op known, it can be decomposed into its normal and shear components by familiar vector operations. Dot Product: OPN = Op. N - Pythagorean Theorem: Ops = - OPN p PN Vi Ps lecture_01.1.nb | 19 Plane P OPNA The PS Also the magnitude of the stress can be calculated from | Op | = 0px + Opy + Op and its direction from Example Consider the case of Point P on a stress-free surface of a body under load. The surface-normal vector at Point P is 21+2 3+k. The stress state internal to the body at Point P is 19xx oxy Oxz Op = Oyx Oyy yz Ozx Ozy Ozz - What are the angles between the surface normal vector and each of the coordinate axes? - What are the relationships between the stresses internal to the body? so We first calculate the vector N which is the surface normal unit vector. N = 1+ 2-2.1 + = 2-2-1 From above Plane P Nx=/= Cos[ex] Ny = m = Cos[ey] N = n = Cos[0] = ArcCos[3] 0x = ArcCos[Nx] = 8y = ArcCos[Ny] = ArcCos[3] 0 = ArcCos[N] = ArcCos[3] 2+1 k In[ ]= ArcCos Out[-]= Out[-]= Out[-]= s[]/ ArcCos ArcCos 2 [31/ / 48.1897 48.1897 If NIMNIM IM 70.5288 1 []/ Then // N Op = 0 Here we have the case illustrated below. // N B // N P Opx = Nx Oxx+Ny ayx+NzOzx 0 = 30x + xy + 0x 20xx+2Oxy + Oxz=0 C If Op = 0 Then Opx = Nx Oxx+Ny ayx + N Ozx 0 = 30xx + xy + 0x 20xx+2 Oxy+0xz = 0 Opy = Nx Oxy+Ny Oyy +Nz Ozy zy 0 = xy + y + 2 Oxy +2 ayy+ Ozy = 0 Opz = Nx Oxz+Ny Oyz + N Ozz 0 = 30x2 + 0y2 +02 20xz+20yz + Oz = 0 Thus the Boundary Conditions are 20xx + 2 Oxy + Oxz=0 2 Oxy+2 ayy+ Ozy = 0 20xz+20yz + Oz = 0 & NO LOAD dis AL TAnd L for small Angles Tan y ~ AL the In Strength of Materials, TE y = WITH LOAD AL Shear Strain, - the symbole is used for Normal Stress, = Normal - the symbol y is used for Shear Stress, y == |Shear In advanced mechanics courses, including this course, the symbole is used for both normal strain and shear strain. Subscripts are used to distinguish strain type and component. Specifically, two subscripts are used. They are defined using a cubic element as shown below. - The first subscript indicates the face of the cube that the strain acts upon (i.e. the "area") - The second subscript indicates the direction of the strain (i.e. the direction of the normal or angular displacement)