A regional airline, Northwest Commuter, has started operating on the west coast of the United States. It has become established as a no-frills airline providing low-cost commuter flights between the west coast cities of Seattle, Portland, and San Francisco. The company has been able to achieve fast turnaround times between flights, but in order to further keep the costs low, the management needs to find new ways for Northwest Commuter to become a more efficient airline. In particular, management wants to start by dropping unprofitable flights and then identifying the most profitable flights.

Imagine that any number of airplanes desired can be leased for now. The leasing and operating costs for each airplane is $30,000 per day, that is incurred (accounted) at 12 midnight every day. At the end of the day, an airplane might remain in the city where it landed on its last flight which does not have any additional daily operating cost (on top of $30,000). Another option is to fly empty overnight to another city to be ready to start a flight from there the next morning. The cost of this latter option is an additional $5,000.

The following table shows the 22 possible flights that are being considered for the coming year. The last column gives the estimated net revenue (with the unit of thousands of dollars) for each flight, given the average number of passengers anticipated for that flight. To simplify the analysis, assume for now that there is virtually no turnaround time between flights so the next flight can begin as soon as the current flight ends. Also, if an immediate next flight is not available, the airplane would wait in the airport until the next scheduled flight from that city.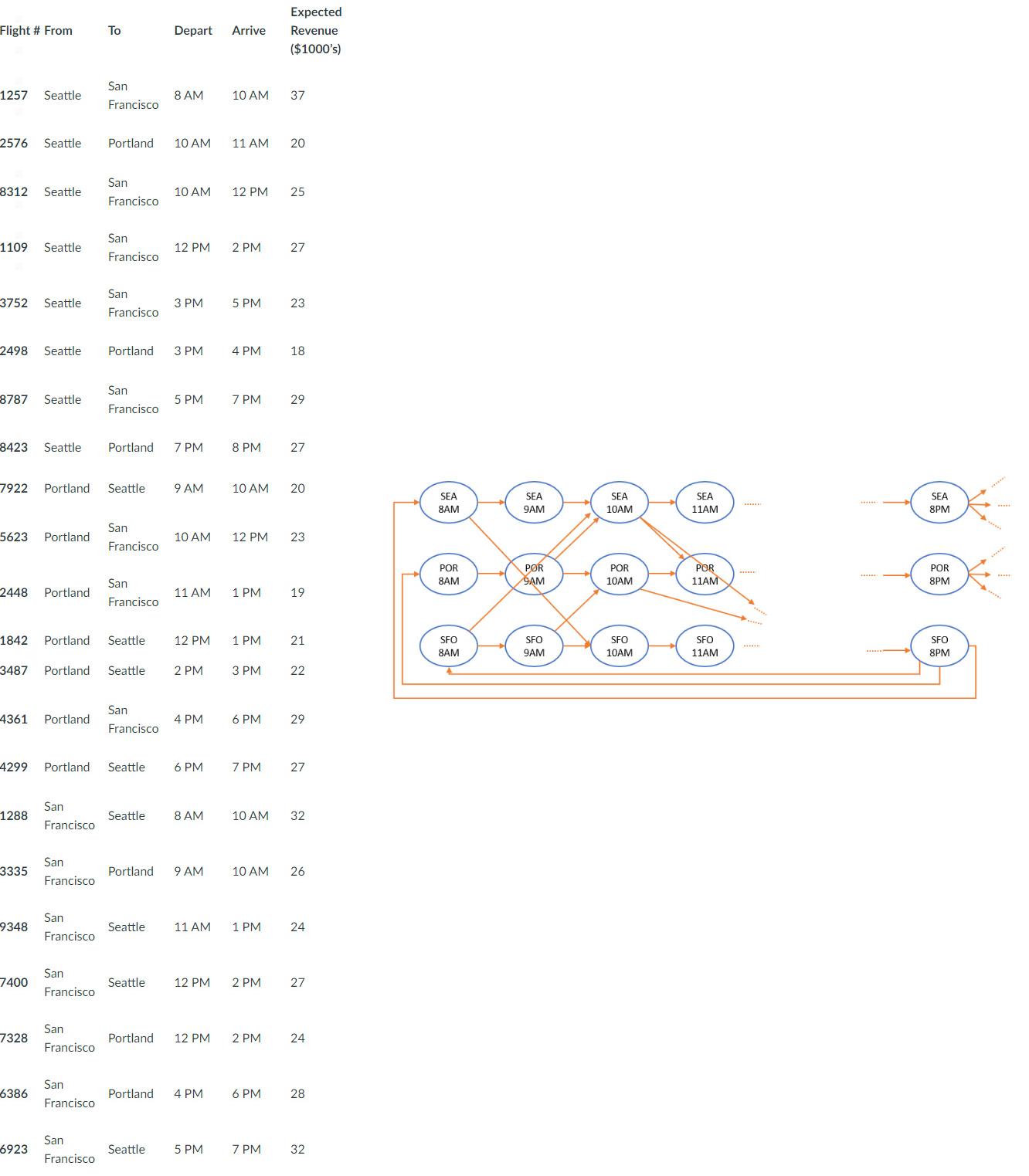

Management developed a network associated with the above flight list that displays the feasible routings of the flights, that is “partially” shown below. There are separate nodes for each combination of city and each hour between 8am to 8pm. The forward cross arcs represent the flight options according to the above table, and the forward horizontal arcs show the option of a plane staying in the same city for the next hour at each point in time. The backward arcs from 8pm to 8am represent the case that airplane remains in the same airport until the next day or fly empty overnight to another city to prepare for the next day.

You are asked to assist in developing a network model that finds the best combination of flights that maximizes the total profit.

In the process of model setup, note the following:

-Since the airplanes are circulating only in the above network, the net-flows of all nodes is 0 (there is no airplane entering from outside the network or exiting the network).

-Each flight as scheduled in the above table cannot be operated by more than one airplane simultaneously.

-Airline is attempting to maximize profit

For now, assume that there is no limit on the number of airplanes that is leased, and the airline can lease any number of airplanes it would like.

Question 1: What is the profit for the flow of one plane along the arc "SEA 10AM" to "POR 11AM"? (enter in the unit of thousands of dollars)

Question 2: What should be the capacity of the flow along the arc "SEA 10AM" to "POR 11AM"? If it can be any large number, enter 1000.

 

 

Expected Flight # From To Depart Arrive Revenue ($1000's) San 1257 Seattle 8 AM 10 AM 37 Francisco 2576 Seattle Portland 10 AM 11 AM 20 San 8312 Seattle 10 AM 12 PM 25 Francisco San 1109 Seattle 12 PM 2 PM 27 Francisco 3752 Seattle San Francisco 3 PM 5 PM 23 2498 Seattle Portland 3 PM 4 PM 18 8787 Seattle San Francisco. 5 PM 7 PM 29 8423 Seattle Portland 7 PM 8 PM 27 7922 Portland Seattle 9 AM 10 AM 20 SEA SEA SEA SEA 8AM 9AM 10AM 11AM San 5623 Portland 10 AM 12 PM 23 Francisco SEA 8PM POR POR POR POR POR 2448 Portland San Francisco 8AM 9AM 10AM 11AM 8PM 11 AM 1 PM 19 1842 Portland Seattle 12 PM 1 PM 21 SFO SFO SFO SFO SFO 8AM 9AM 10AM 11AM 8PM 3487 Portland Seattle 2 PM 3 PM 22 San 4361 Portland 4 PM 6 PM 29 Francisco 4299 Portland Seattle 6 PM 7 PM 27 San 1288 Seattle 8 AM 10 AM 32 Francisco San 3335 Portland 9 AM 10 AM 26 Francisco San 9348 Seattle 11 AM 1 PM 24 Francisco San 7400 Seattle 12 PM 2 PM Francisco San 7328 Portland 12 PM 2 PM Francisco 27 24 24 24 6386 San Francisco Portland 4 PM 6 PM 28 6923 San Francisco Seattle 5 PM 7 PM 32 32