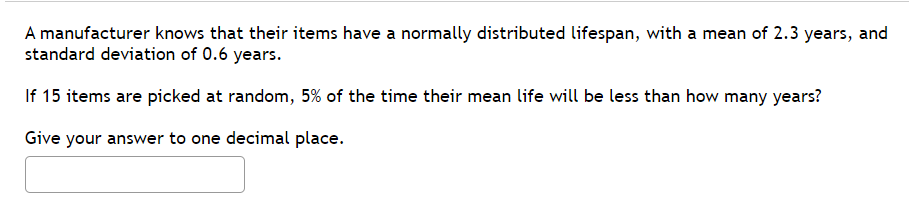
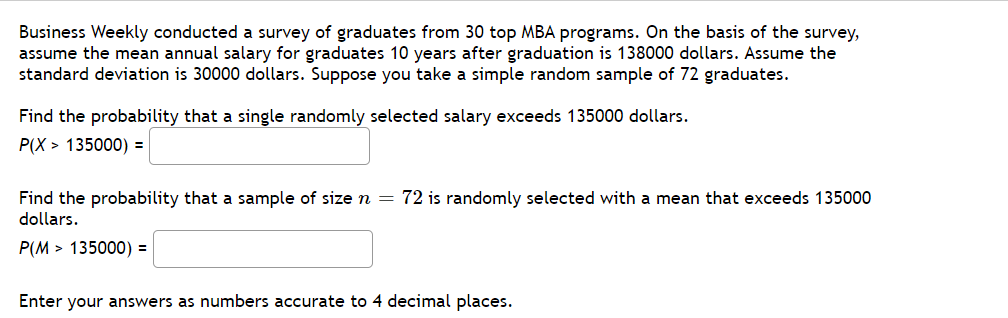
A simple random sample of size n=15 is obtained from a population of student heights that is normally distributed with a mean of 69.6 inches and a standard deviation of 3.5 inches. Is the sampling distribution normally distributed? Why?

• Yes, the sampling distribution is normally distributed because the population is normally distributed.
• Yes, the sampling distribution is normally distributed because the population mean is greater than 30.
• No, the sampling distribution is not normally distributed because the population is not normally distributed.

Which of the following is true about the sampling distribution of means?

• Sampling distributions of means are always nearly normal.
• Sampling distribution of the mean is always right skewed since means cannot be smaller than 0.
• Shape of the sampling distribution of means is always the same shape as the population distribution, no matter what the sample size is.

Sampling distributions of means get closer to normality as the sample size increases.

----------------------------------------------------------------------------------------------------------

Which of the following is NOT a property of the sampling distribution of the sample mean?

• The distribution of the sample mean tends to be skewed to the right or left.
• The expected value of the sample mean is equal to the population mean.
• The sample means target the value of the population mean.

Which of the following is NOT a conclusion of the Central Limit Theorem?

• The mean of all sample means is the population mean.
• The standard deviation of all sample means is the population standard deviation divided by the square root of the sample size.
• The distribution of the sample data will approach a normal distribution as the sample size increases.
• The distribution of the sample means will, as the sample size increases, approach a normal distribution.

----------------------------------------------------------------------------------------------------------

The Central Limit Theorem is used when dealing with:

• chi-squared distributions
• mean from a sample
• sampling distribution of a standard deviation
• individual data point

----------------------------------------------------------------------------------------------------------

When using the CLT, we use?/?nfor the:

• sample size
• mean for the sample
• standard deviation of the sample means
• standard deviation for individual value

----------------------------------------------------------------------------------------------------------

We have a population that consists of the full height of a certain species of tree. Assume that the population has a normal distribution with ,u. = 75 ft and o' = 14.2 ft. You intend to measure a random sample of n = 224 trees. What is the mean of the distribution of sample means? What is the standard deviation of the distribution of sample means (i.e., the standard error in estimating the mean}? {Report answer accurate to 2 decimal places.) A population of values has a normal distribution with p. = 71.9 and or = 68. You intend to draw a random sample of size n = 155. What is the mean of the distribution of sample means? What is the standard deviation of the distribution of sample means? {Report answer accurate to 2 decimal places.) 05,: Acompany produces steel rods. The lengths of the steel rods are normally distributed with a mean of 119.4-cm and a standard deviation of 1.3-cm. For shipment, 11 steel rods are bundled together. Find the probability that the average length of a randomly selected bundle of steel rods is less than 119.8- cm. P(M 135000} = Find the probability that a sample of size n = 72 is randomly selected with a mean that exceeds 135000 dollars. Enter your answers as numbers accurate to 4 decimal places. A leading magazine (like Barron's) reported at one time that the average number of weeks an individual is unemployed is 33 weeks. Assume that for the population of all unemployed individuals the population mean length of unemployment is 38 weeks and that the population standard deviation is 2 weeks. Suppose you would like to select a random sample of 3D unemployed individuals for a follow-up study. Find the probability that a single randomly selected value is less than 39. P(X 993} = [ l Find the probability that a sample of size n = 54 is randomly selected with a mean that exceeds 993 dollars. PM > 993} = Enter your answers as numbers accurate to 4 decimal places. The lengths of pregnancies in a small rural village are normally.r distributed with a mean of 264 days and a standard deviation of 16 days. A distribution of values is normal with a mean of 264 and a standard deviation of 16. What percentage of pregnancies last fewer than 310 days? P(X 71.1]= Enter your answers as numbers accurate to 4 decimal places. Acompany produces steel rods. The lengths of the steel rods are normallyr distributed with a mean of 132.4cm and a standard deviation of 2.3-cm. Find the probability that the length of a randomly selected steel rod is less than 132.6-cm. P(X 544.4} = Enter your answer as a number accurate to 4 decimal places. If the random sample of 13 men does result in a mean score of 544.4, is there strong evidence to support the claim that the course is actually effective? 0 Yes. The probability indicates that is is unlikely that by chance, a randomly selected group of students would get a mean as high as 544.4. 0 No. The probability indicates that is is possible by chance alone to randomly select a group of students with a mean as high as 544.4