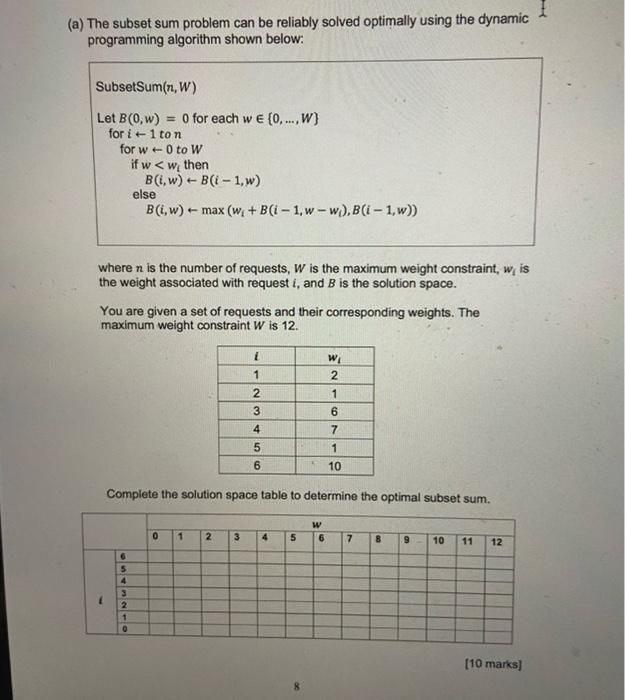
Question: (a) The subset sum problem can be reliably solved optimally using the dynamic programming algorithm shown below: SubsetSum (n,W) Let B(0,w)=0 for each w{0,,W} for
(a) The subset sum problem can be reliably solved optimally using the dynamic programming algorithm shown below: SubsetSum (n,W) Let B(0,w)=0 for each w{0,,W} for i1 ton for w0 to W if waN) return q else return aN State what problem this algorithm solves and write down the two recurrence equations that characterise this recursive algorithm. [10 marks] (c) Define what is meant by the term "topological sort" when applied to a Directed Acyclic Graph (DAG). [5 marks] (d) Enumerate all possible topological sorts for the DAG shown below. (e) The Ford-Fulkerson ajgorithm is used to determine network flow. The diagram below represents a data network that connects a Data Service Provider (DSP) connected to v1(s) to a customer connected to v6(t). Each edge represents a single data transmission link. The notation p/q indicates a current actual forwards flow p measured in Gb/s in a cable with a maximum capacity of q also measured in Gb/s. At the outset no data is being sent by the DSP to the customer. i. Show the residual graph that will be created from the initial empty flow. When drawing the residual graph, show a forward edge with capacity x and a backward edge with flow y by annotating the edge x;y^. [2 marks] ii. What is the bottleneck edge of the path (s,v3,v2,v5,t) in the residual graph you have given in answer to part (i)? [2 marks] iii. Show the residual graph after incorporating the simple path (s,v3,v2,vs,t) that results from augmenting the flow based on the residual graph you have given in answer to part (i). [4 marks] iv. Repeat the process outlined above incorporating additionally the simple paths (s,v2,v1,v5,t),(s,v3,v4,v2,vst),(s,v2,v4,t) and (s,v3,v4,t) showing each residual graph, to determine the maximum flow between s and t, and thus the maximum data bandwidth that can be achieved between the DSP and the customer. Remember to check whether you are following a forwards or backwards edge in the residual graph