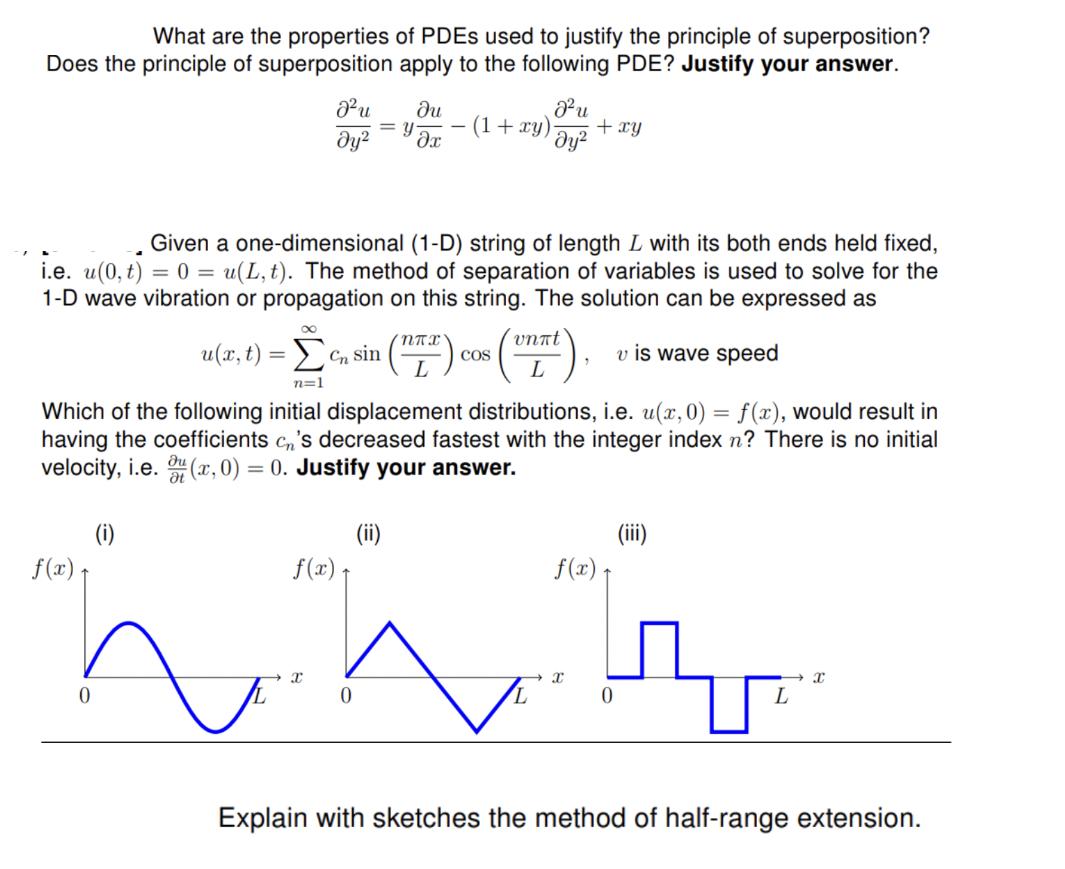
What are the properties of PDEs used to justify the principle of superposition? Does the principle of superposition apply to the following PDE? Justify your answer. f(x) t Ju dy 0 (i) Given a one-dimensional (1-D) string of length L with its both ends held fixed, i.e. u(0, t) = 0 = u(L, t). The method of separation of variables is used to solve for the 1-D wave vibration or propagation on this string. The solution can be expressed as u(x, t) = sin = y f(x) + 0 (ii) (1 + xy) nx Ju dy COS n=1 Which of the following initial displacement distributions, i.e. u(x, 0) = f(x), would result in having the coefficients c's decreased fastest with the integer index n? There is no initial velocity, i.e. (x,0) = 0. Justify your answer. nit). vnt + xy f(x) X v is wave speed 0 (iii) I Explain with sketches the method of half-range extension.