A warehouse, similar to Ocados algorithm-controlled warehouse, has a despatch area and a vast storage area divided into zones. Requested items are brought to despatch from the storage area by an automatic picking system. An automated crate travels along tracks from despatch to the appropriate storage area zones, and back to despatch. Tracks are in pairs that allow the crate to travel in either direction.

The crate may need to pass through other zones to get to and from the zones where the requested items are.

The warehouse can be represented by a weighted digraph. Nodes represent the despatch and storage zones. Weighted edges represent tracks between the despatch and storage zones, and between zones. A weight represents the time (in seconds) that it takes to travel between the two zones joined by the edge.

A weighted digraph that represents an example warehouse:

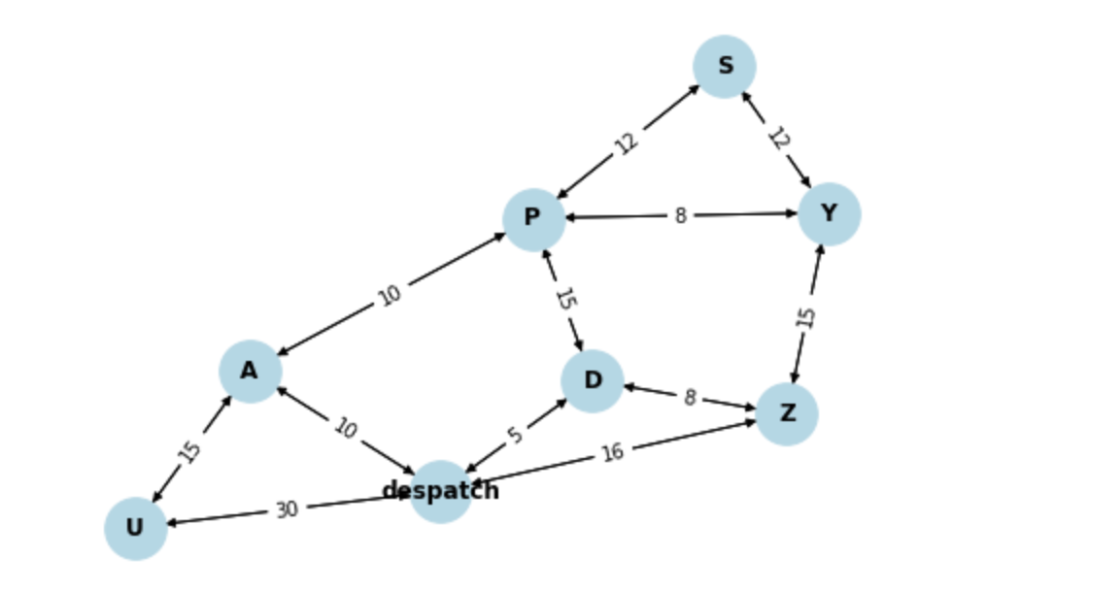
PLEASE DO NOT COPY AND PASTE AN ANSWER FROM ANOTHER QUESTION.

Q4

In this part we explore the problem of finding the quickest route from one zone to another; that is, finding a shortest path on the graph.

Q4(a)(i)

State why the graph representing the warehouse should be connected.

Q4(a)(ii)

State why the problem of finding the shortest path from one zone to another is not the travelling salesman problem (TSP).

Q4(a)(iii)

State why the problem of finding the shortest path from one zone to another is not about finding a minimum spanning tree of the graph.

Use Dijsktra's algorithm to compute a shortest path from despatch to each zone. Draw the resulting tree.

The contents of Q4_warehouse.py are reproduced below for your reference.

warehouse = WeightedDiGraph() warehouse.add_node('despatch') warehouse.add_node('A') warehouse.add_node('D') warehouse.add_node('P') warehouse.add_node('S') warehouse.add_node('U') warehouse.add_node('Y') warehouse.add_node('Z')

warehouse.add_edge('despatch','U',30) warehouse.add_edge('U','despatch',30) warehouse.add_edge('despatch','A',10) warehouse.add_edge('A','despatch',10) warehouse.add_edge('despatch','D',5) warehouse.add_edge('D','despatch',5) warehouse.add_edge('despatch','Z',16) warehouse.add_edge('Z','despatch',16) warehouse.add_edge('A','U',15) warehouse.add_edge('U','A',15) warehouse.add_edge('A','P',10) warehouse.add_edge('P','A',10) warehouse.add_edge('P','S',12) warehouse.add_edge('S','P',12) warehouse.add_edge('D','Z',8) warehouse.add_edge('Z','D',8) warehouse.add_edge('P','D',15) warehouse.add_edge('D','P',15) warehouse.add_edge('P','Y',8) warehouse.add_edge('Y','P',8) warehouse.add_edge('Y','S',12) warehouse.add_edge('S','Y',12) warehouse.add_edge('Y','Z',15) warehouse.add_edge('Z','Y',15)

warehouse.draw()

# Write your code here

Q4(a)(v)

Here is a definition of a function that, given a connected weighted digraph, finds the shortest path from a given start node to a given end node.

Function: shortest path between nodes Inputs: warehouse, a weighted digraph; start, a node; end, a node Preconditions: start and end are different nodes in warehouse; warehouse is connected Output: path, a sequence of nodes Postconditions: path is the shortest path from start to end in warehouse

Here is a description of an algorithm that solves the shortest path between nodes problem.

Use Dijkstra's algorithm to construct a tree of shortest paths from start to every other node of warehouse.

Let path be the sequence [end].

In the tree, starting with end visit the in-neighbour of the node, then the in-neighbour of that node, and so on, until getting to start, appending each node to path.

Reverse the sequence path using reverse_in_place() (Note: The code for reverse_in_place() is reproduced in Q4(a)(vi).)

Analyse the worst-case complexity of this algorithm for a connected weighted digraph warehousewith n nodes and e edges, explaining the worst-case complexity of each step as well as the overall complexity. You should assume that the graph is represented as adjacency sets of out-neighbours.

Q4(a)(vi)

Implement this shortest path between nodes algorithm as a function in Python. Include a docstring. We have provided the reverse_in_place() code. Make sure that your function inputs are in the order warehouse, start, end.

Test your implementation by running the test code given below. If any tests fail, then debug your implementation and run the test code again. You can repeat this iterative process as many times as you want. If there are any tests that fail and you are unable to identify the problem, you may add explanatory comments below the test code.

%run -i m269_util def reverse_in_place(values: list) -> None: """Reverse the order of the values.

Postconditions: post-values = [pre-values[len(pre-values) - 1], ..., pre-values[1], pre-values[0]] """ left_index = 0 right_index = len(values) - 1 while left_index

# Write your function code here

# Test code shortest_path_tests = [ # case, warehouse, start, end, shortest path ('neighbouring zones', warehouse, 'S', 'Y', ['S','Y']), ('zone neighbouring despatch', warehouse, 'despatch', 'D', ['despatch','D']), ('zone neighbouring despatch shortest path not direct', warehouse, 'despatch','Z', ['despatch','D','Z']), ('distant zones', warehouse, 'U', 'D', ['U','A','despatch','D']), ('distant zones opposite direction', warehouse, 'D', 'U', ['D','despatch','A','U']), ('two different shortest paths, choice depends on dijkstra', warehouse, 'Z', 'P', ['Z','D','P']), ] test(shortest_path_between_nodes, shortest_path_tests) # Add any explanatory comments here

In this part we explore the problem of taking the quickest route from despatch to visit a given set of zones in any order (to fetch the requested items) before returning to despatch.

For example, the quickest route from despatch to visit D and Z in any order before returning to despatch is: despatch, D, Z, D, despatch.

Q4(b)(i)

State why this problem is not the travelling salesman problem (TSP).

Q4(b)(ii)

We could use brute force to generate all possible candidate routes and choose the quickest one. State why this is not a practical option for routes through a large number of zones.

Q4(b)(iii)

We can approach the problem in a greedy way by visiting the zones in the order they are listed.

Here is a greedy algorithm that visits the zones in the order in which they are listed, taking the shortest path to the next zone in the list each time:

let listed zones be the list of at least two zones to visit

visit the first zone in listed zones by the shortest path from despatch

for each zone in listed zones visit the next zone in the list by the shortest path from the previous zone in the list

return to despatch by the shortest path from the last zone in listed zones

Find a counter-example list of three zones for the example warehouse graph to show that this greedy algorithm is not correct. Explain how you arrived at your counter-example.

Give the route the greedy algorithm will take, explaining why it's that route. Give the quickest route you can find for your counter-example.

Calculate, by looking at the graph, how many seconds the route taken by the greedy algorithm will take, and how many seconds your quickest route will take.

Q4(b)(iv)

An alternative greedy way to approach this problem is to visit the closest (in time) zone in the set from the current zone by the shortest path at each step.

Here is a greedy algorithm that visits the closest (in time) zone in the set from the current zone by the shortest path each time, removing the zone from the set once it has been visited:

let zones to visit be the set of at least two zones to visit

let current be despatch

while zones to visit is not empty:

let nearest be the nearest zone in zones to visit to current

visit nearest by the shortest path from current

remove nearest from zones to visit

let current be nearest

return to despatch by the shortest path from current

What route will this greedy algorithm take for the counter-example you found in part (b)(iii)? Explain why it's that route.

Which of the two greedy algorithms appears to be a better solution for the problem of taking the quickest route from despatch to visit a given set of zones in any order before returning to despatch? Give a reason.

What else do you need to analyse to support your design choice between the two greedy algorithms?