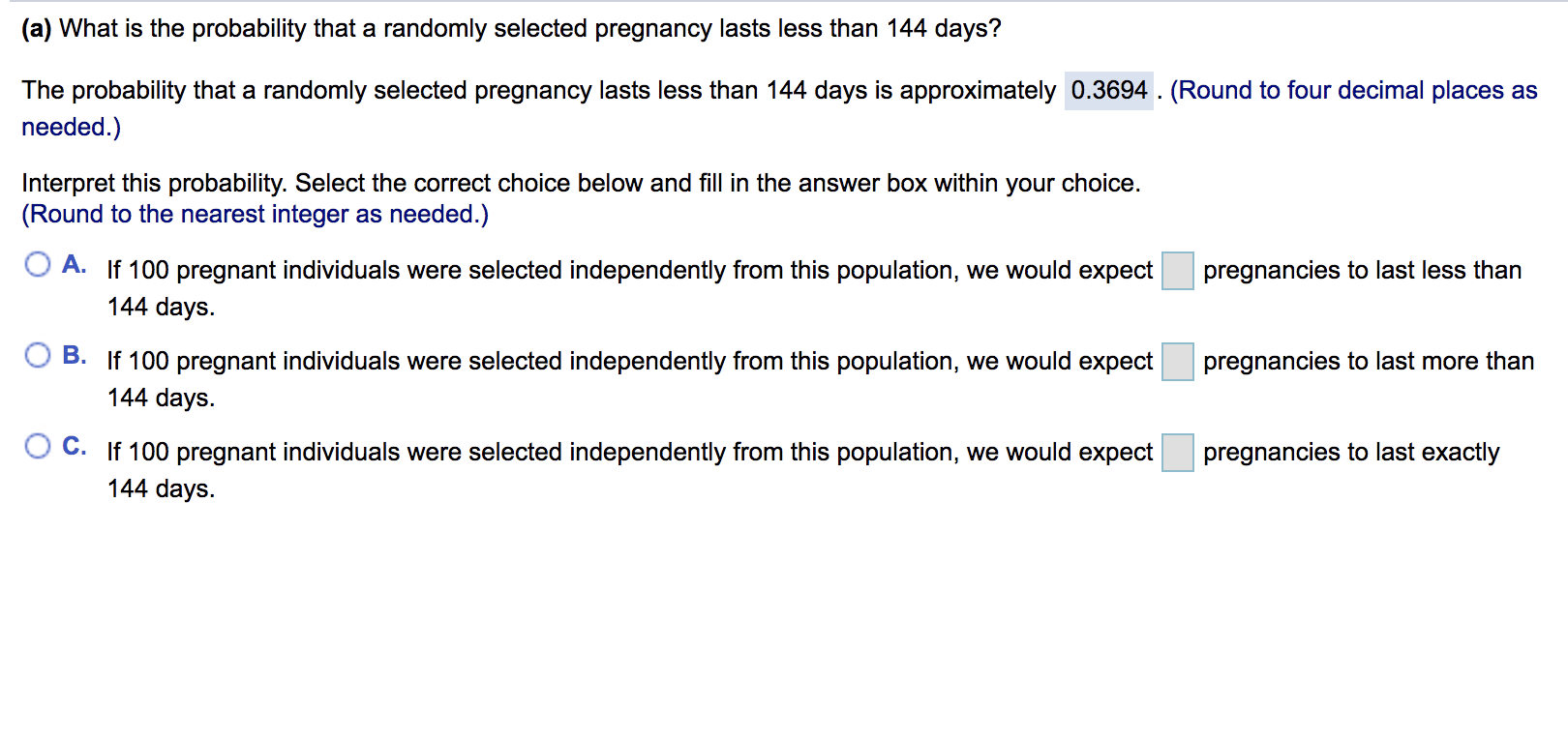
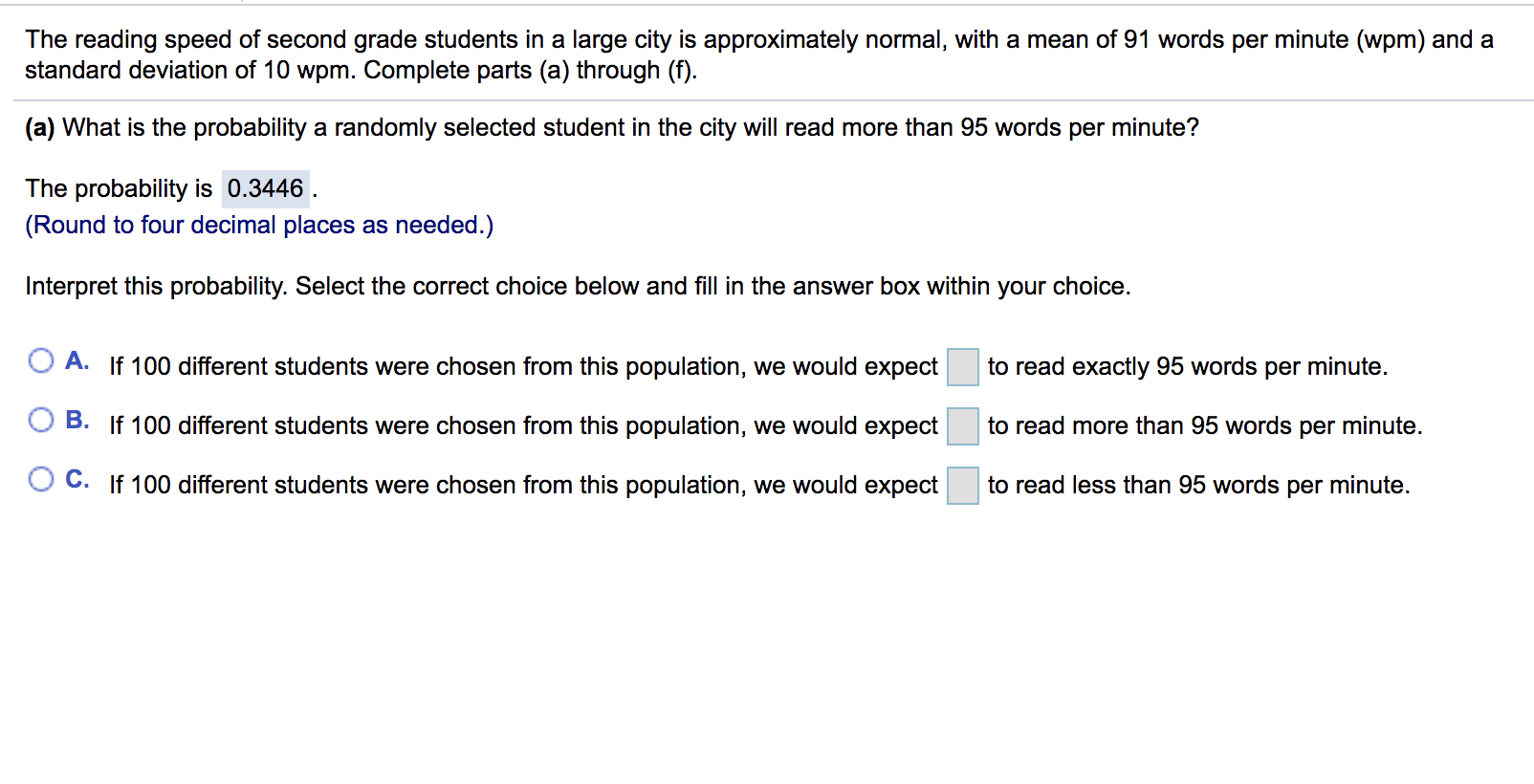
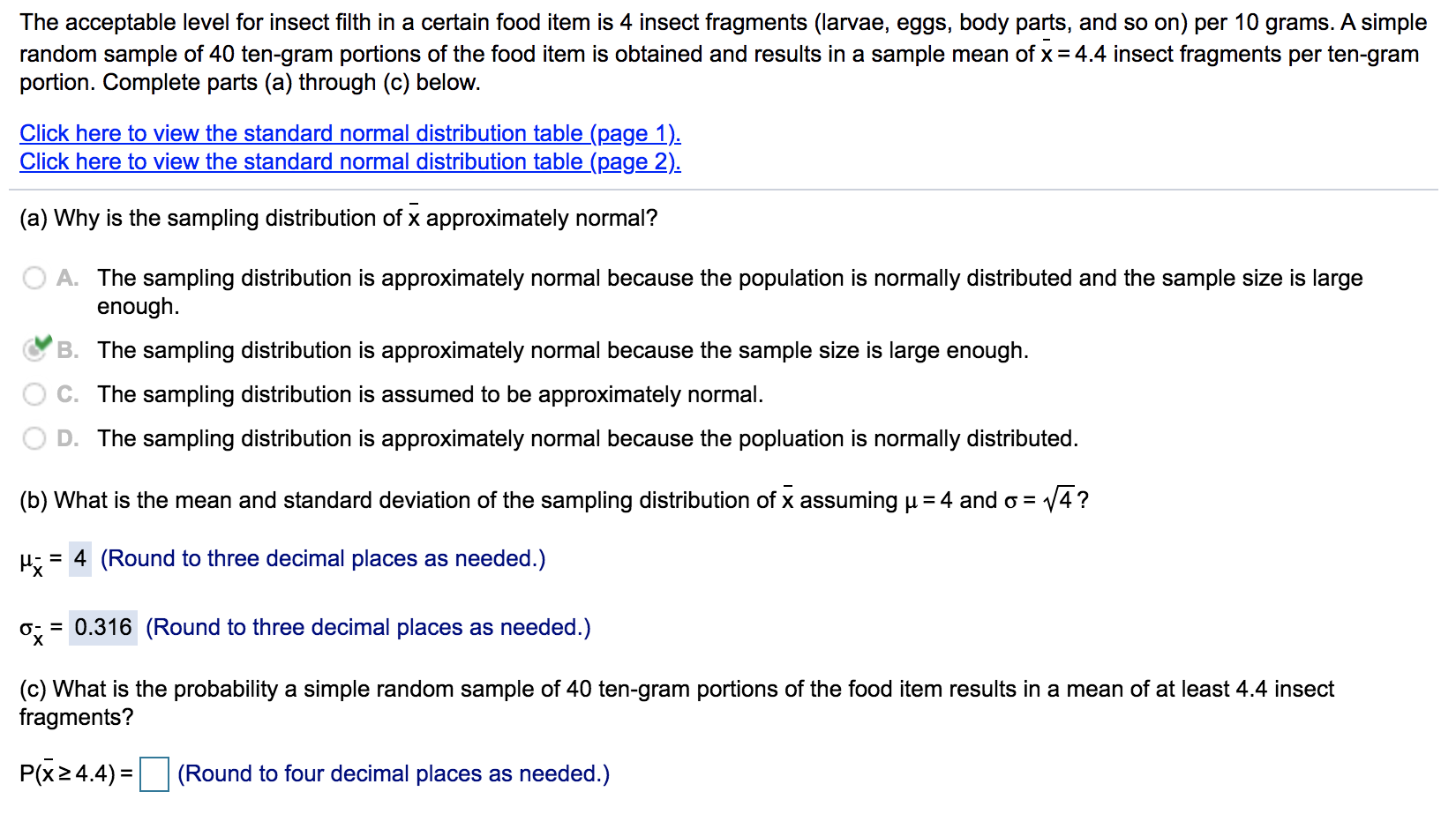
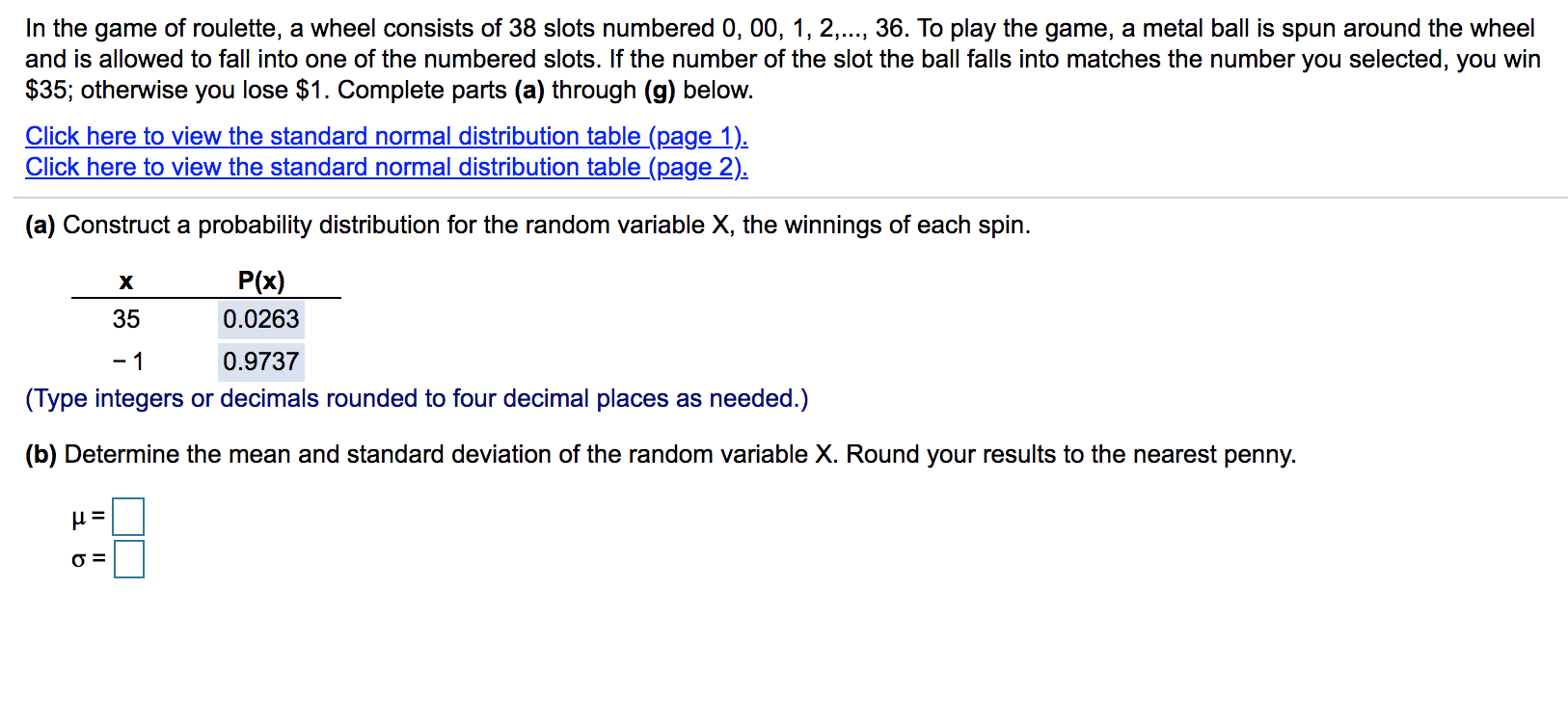
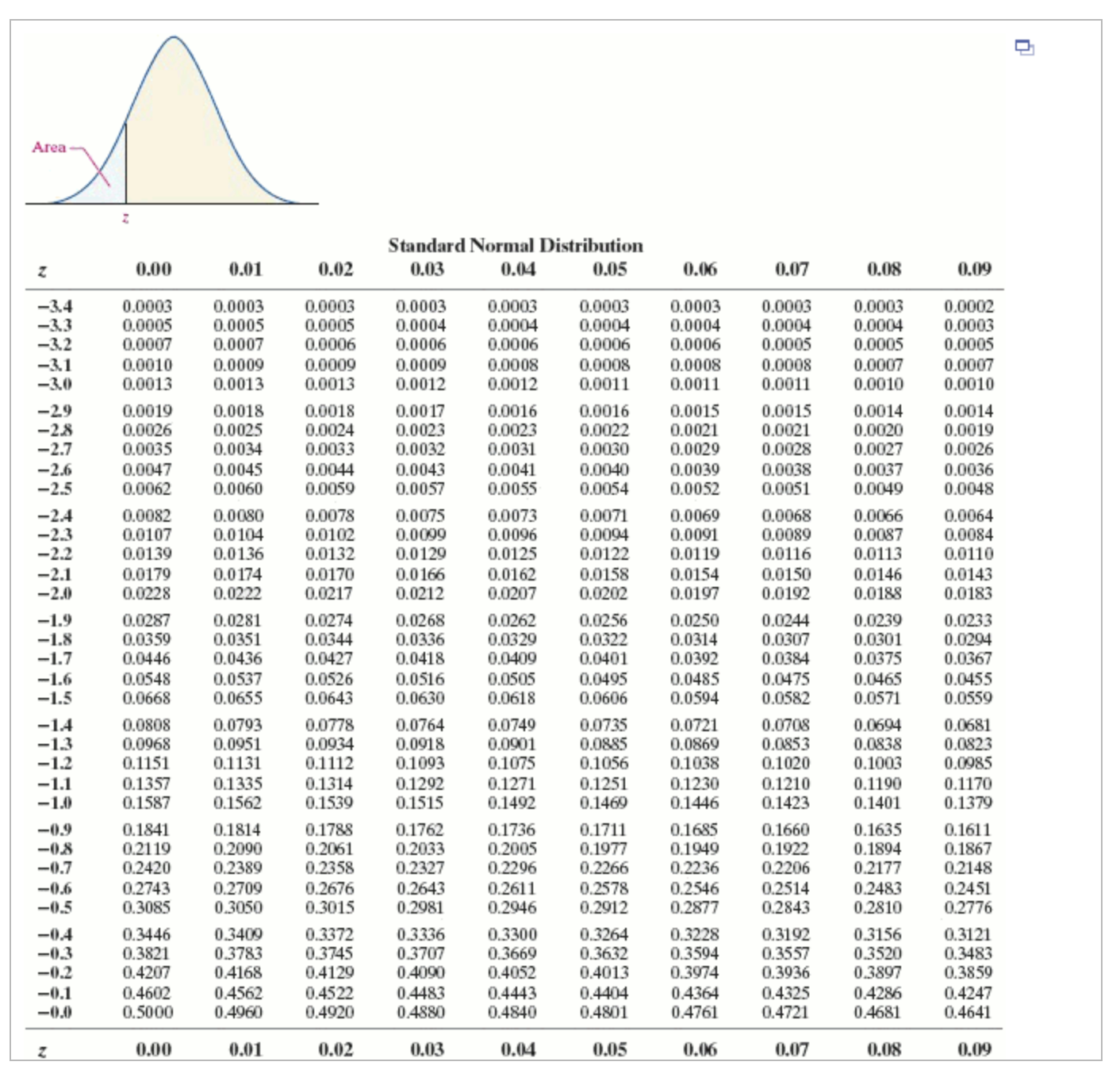
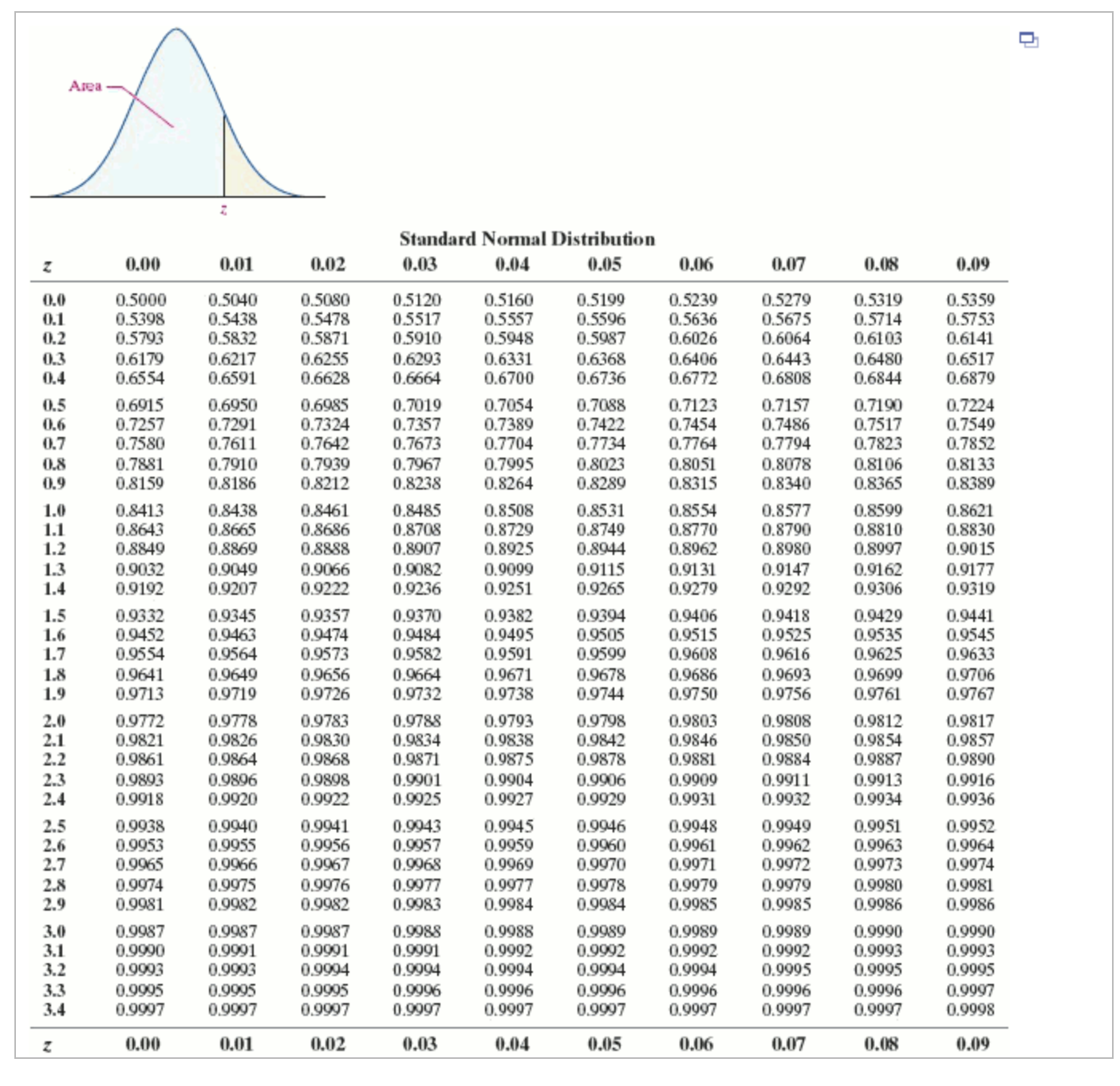
(a) What is the probability that a randomly selected pregnancy lasts less than 144 days? The probability that a randomly selected pregnancy lasts less than 144 days is approximately 0.3694. (Round to four decimal places as needed.) Interpret this probability. Select the correct choice below and fill in the answer box within your choice. (Round to the nearest integer as needed.) A. If 100 pregnant individuals were selected independently from this population, we would expect 144 days. pregnancies to last less than B. If 100 pregnant individuals were selected independently from this population, we would expect 144 days. pregnancies to last more than C. If 100 pregnant individuals were selected independently from this population, we would expect 144 days. pregnancies to last exactly The reading speed of second grade students in a large city is approximately normal, with a mean of 91 words per minute (wpm) and a standard deviation of 10 wpm. Complete parts (a) through (f). (a) What is the probability a randomly selected student in the city will read more than 95 words per minute? The probability is 0.3446. (Round to four decimal places as needed.) Interpret this probability. Select the correct choice below and fill in the answer box within your choice. A. If 100 different students were chosen from this population, we would expect B. If 100 different students were chosen from this population, we would expect OC. If 100 different students were chosen from this population, we would expect to read exactly 95 words per minute. to read more than 95 words per minute. to read less than 95 words per minute. Suppose a geyser has a mean time between eruptions of 74 minutes. Let the interval of time between the eruptions be normally distributed with standard deviation 21 minutes. Complete parts (a) through (e) below. (a) What is the probability that a randomly selected time interval between eruptions is longer than 84 minutes? The probability that a randomly selected time interval is longer than 84 minutes is approximately 0.3170. (Round to four decimal places as needed.) (b) What is the probability that a random sample of 7 time intervals between eruptions has a mean longer than 84 minutes? The probability that the mean of a random sample of 7 time intervals is more than 84 minutes is approximately (Round to four decimal places as needed.) The acceptable level for insect filth in a certain food item is 4 insect fragments (larvae, eggs, body parts, and so on) per 10 grams. A simple random sample of 40 ten-gram portions of the food item is obtained and results in a sample mean of x = 4.4 insect fragments per ten-gram portion. Complete parts (a) through (c) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) Why is the sampling distribution of x approximately normal? A. The sampling distribution is approximately normal because the population is normally distributed and the sample size is large enough. B. The sampling distribution is approximately normal because the sample size is large enough. C. The sampling distribution is assumed to be approximately normal. D. The sampling distribution is approximately normal because the popluation is normally distributed. = 4? (b) What is the mean and standard deviation of the sampling distribution of x assuming = 4 and = = 4 (Round to three decimal places as needed.) = 0.316 (Round to three decimal places as needed.) (c) What is the probability a simple random sample of 40 ten-gram portions of the food item results in a mean of at least 4.4 insect fragments? P(x4.4)= (Round to four decimal places as needed.) In the game of roulette, a wheel consists of 38 slots numbered 0, 00, 1, 2,..., 36. To play the game, a metal ball is spun around the wheel and is allowed to fall into one of the numbered slots. If the number of the slot the ball falls into matches the number you selected, you win $35; otherwise you lose $1. Complete parts (a) through (g) below. Click here to view the standard normal distribution table (page 1). Click here to view the standard normal distribution table (page 2). (a) Construct a probability distribution for the random variable X, the winnings of each spin. x 35 -1 P(x) 0.0263 0.9737 (Type integers or decimals rounded to four decimal places as needed.) (b) Determine the mean and standard deviation of the random variable X. Round your results to the nearest penny. Suppose Jack and Diane are each attempting to use a simulation to describe the sampling distribution from a population that is skewed left with mean 70 and standard deviation 10. Jack obtains 1000 random samples of size n = 5 from the population, finds the mean of the means, and determines the standard deviation of the means. Diane does the same simulation, but obtains 1000 random samples of size n = 30 from the population. Complete parts (a) through (c) below. (a) Describe the shape you expect for Jack's distribution of sample means. Describe the shape you expect for Diane's distribution of sample means. Choose the correct answer below. A. Jack's distribution and Diane's distribution are expected to be approximately normal. However, Jack's will have a greater standard deviation. B. Jack's distribution is expected to be skewed left, but not as much as the original distribution. Diane's distribution is expected to be approximately normal. C. Jack's distribution is expected to be skewed right, but not as much as the original distribution. Diane's distribution is expected to be approximately normal. D. Diane's distribution is expected to be skewed left, but more than the original distribution. Jack's distribution is expected to be approximately normal. (b) What do you expect the mean of Jack's distribution to be? What do you expect the mean of Diane's distribution to be? Jack's distribution is expected to have a mean of 70. Diane's distribution is expected to have a mean of 70 . (c) What do you expect the standard deviation of Jack's distribution to be? What do you expect the standard deviation of Diane's distribution to be? Jack's distribution is expected to have a standard deviation of Diane's distribution is expected to have a standard deviation of (Round to two decimal places as needed.) Area Z n Standard Normal Distribution 2 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 -3.4 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0003 0.0002 -3.3 0.0005 0.0005 0.0005 0.0004 0.0004 0.0004 0.0004 0.0004 0.0004 0.0003 -3.2 0.0007 0.0007 0.0006 0.0006 0.0006 0.0006 0.0006 0.0005 0.0005 0.0005 -3.1 0.0010 0.0009 0.0009 0.0009 0.0008 0.0008 0.0008 0.0008 0.0007 0.0007 -3.0 0.0013 0.0013 0.0013 0.0012 0.0012 0.0011 0.0011 0.0011 0.0010 0.0010 -29 0.0019 0.0018 0.0018 0.0017 0.0016 0.0016 0.0015 0.0015 0.0014 0.0014 -2.8 0.0026 0.0025 0.0024 0.0023 0.0023 0.0022 0.0021 0.0021 0.0020 0.0019 -2.7 0.0035 0.0034 0.0033 0.0032 0.0031 0.0030 0.0029 0.0028 0.0027 0.0026 -2.6 0.0047 0.0045 0.0044 0.0043 0.0041 0.0040 0.0039 0.0038 0.0037 0.0036 -2.5 0.0062 0.0060 0.0059 0.0057 0.0055 0.0054 0.0052 0.0051 0.0049 0.0048 2.4 0.0082 0.0080 0.0078 0.0075 0.0073 0.0071 0.0069 0.0068 0.0066 0.0064 -2.3 0.0107 0.0104 0.0102 0.0099 0.0096 0.0094 0.0091 0.0089 0.0087 0.0084 -2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110 -2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 0.0146 0.0143 -2.0 0.0228 0.0222 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183 -1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 0.0244 0.0239 0.0233 -1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294 -1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367 -1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.0485 0.0475 0.0465 0.0455 -1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559 -14 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681 1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823 -1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170 1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379 -0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611 -0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867 -0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148 -0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451 -0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776 -0.4 0.3446 0.3409 0.3372 0.3336 0.3300 0.3264 0.3228 0.3192 0.3156 0.3121 -0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483 -0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859 -0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247 -0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641 Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 Area Standard Normal Distribution n Z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 2.0 2.7 2.9 999999 999999 9233 39939 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 0.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 0.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.6103 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 0.6808 0.6844 0.6879 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7088 0.7123 0.7157 0.7190 0.7224 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 0.8340 0.8365 0.8389 1.0 0.8413 0.8438 0.8461 0.8485 0.8508 0.8531 0.8554 0.8577 0.8599 0.8621 1.1 0.8643 0.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 0.8810 0.8830 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.8997 0.9015 1.3 0.9032 0.9049 0.9066 0.9082 0.9099 0.9115 0.9131 0.9147 0.9162 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 0.9251 0.9265 0.9279 0.9292 0.9306 0.9319 1.5 0.9332 0.9345 0.9357 0.9370 0.9382 0.9394 0.9406 0.9418 0.9429 0.9441 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 0.9744 0.9750 0.9756 0.9761 0.9767 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 2.1 0.9821 0.9826 0.9830 0.9834 0.9838 0.9842 0.9846 0.9850 0.9854 0.9857 2.2 0.9861 0.9864 0.9868 0.9871 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 0.9893 0.9896 0.9898 0.9901 0.9904 0.9906 0.9909 0.9911 0.9913 0.9916 2.4 0.9918 0.9920 0.9922 0.9925 0.9927 0.9929 0.9931 0.9932 0.9934 0.9936 2.5 0.9938 0.9940 0.9941 0.9943 0.9945 0.9946 0.9948 0.9949 0.9951 0.9952 2.6 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 0.9964 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 2.8 0.9974 0.9975 0.9976 0.9977 0.9977 0.9978 0.9979 0.9979 0.9980 0.9981 0.9981 0.9982 0.9982 0.9983 0.9984 0.9984 0.9985 0.9985 0.9986 0.9986 3.0 0.9987 0.9987 0.9987 0.9988 0.9988 0.9989 0.9989 0.9989 0.9990 0.9990 3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 3.2 0.9993 0.9993 0.9994 0.9994 0.9994 0.9994 0.9994 0.9995 0.9995 0.9995 3.3 0.9995 0.9995 0.9995 0.9996 0.9996 0.9996 0.9996 0.9996 0.9996 0.9997 3.4 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9997 0.9998 z 0.00 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09