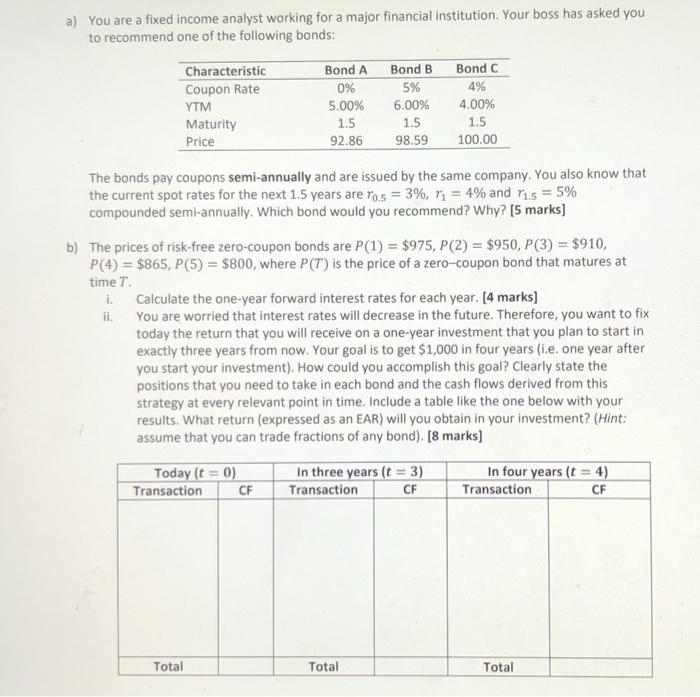
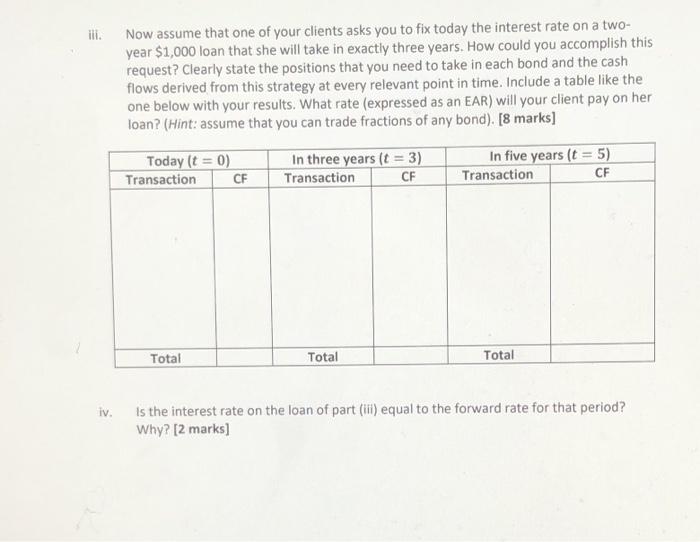
a) You are a fixed income analyst working for a major financial institution. Your boss has asked you to recommend one of the following bonds: Characteristic Coupon Rate YTM Maturity Price Bond A 0% 5.00% 1.5 92.86 Bond B 5% 6.00% 1.5 98.59 Bond C 4% 4.00% 1.5 100.00 The bonds pay coupons semi-annually and are issued by the same company. You also know that the current spot rates for the next 1.5 years are 70.5 = 3%, 11 = 4% and 715 = 5% compounded semi-annually. Which bond would you recommend? Why? [5 marks] b) The prices of risk-free zero-coupon bonds are P(1) = $975, P(2) = $950, P(3) = $910, P(4) = $865, P(5) = $800, where P(T) is the price of a zero-coupon bond that matures at time T. i Calculate the one-year forward interest rates for each year. [4 marks] il. You are worried that interest rates will decrease in the future. Therefore, you want to fix today the return that you will receive on a one-year investment that you plan to start in exactly three years from now. Your goal is to get $1,000 in four years (ie, one year after you start your investment). How could you accomplish this goal? Clearly state the positions that you need to take in each bond and the cash flows derived from this strategy at every relevant point in time. Include a table like the one below with your results. What return (expressed as an EAR) will you obtain in your investment? (Hint: assume that you can trade fractions of any bond). (8 marks] Today (t = 0) Transaction CF In three years (t = 3) Transaction CF In four years (t = 4) Transaction CF Total Total Total ill. Now assume that one of your clients asks you to fix today the interest rate on a two- year $1,000 loan that she will take in exactly three years. How could you accomplish this request? Clearly state the positions that you need to take in each bond and the cash flows derived from this strategy at every relevant point in time. Include a table like the one below with your results. What rate (expressed as an EAR) will your client pay on her loan? (Hint: assume that you can trade fractions of any bond). [8 marks] Today (t = 0) Transaction CF In three years (t = 3) Transaction CF In five years (t = 5) Transaction CF Total Total Total iv. Is the interest rate on the loan of part (ill) equal to the forward rate for that period? Why? [2 marks] a) You are a fixed income analyst working for a major financial institution. Your boss has asked you to recommend one of the following bonds: Characteristic Coupon Rate YTM Maturity Price Bond A 0% 5.00% 1.5 92.86 Bond B 5% 6.00% 1.5 98.59 Bond C 4% 4.00% 1.5 100.00 The bonds pay coupons semi-annually and are issued by the same company. You also know that the current spot rates for the next 1.5 years are 70.5 = 3%, 11 = 4% and 715 = 5% compounded semi-annually. Which bond would you recommend? Why? [5 marks] b) The prices of risk-free zero-coupon bonds are P(1) = $975, P(2) = $950, P(3) = $910, P(4) = $865, P(5) = $800, where P(T) is the price of a zero-coupon bond that matures at time T. i Calculate the one-year forward interest rates for each year. [4 marks] il. You are worried that interest rates will decrease in the future. Therefore, you want to fix today the return that you will receive on a one-year investment that you plan to start in exactly three years from now. Your goal is to get $1,000 in four years (ie, one year after you start your investment). How could you accomplish this goal? Clearly state the positions that you need to take in each bond and the cash flows derived from this strategy at every relevant point in time. Include a table like the one below with your results. What return (expressed as an EAR) will you obtain in your investment? (Hint: assume that you can trade fractions of any bond). (8 marks] Today (t = 0) Transaction CF In three years (t = 3) Transaction CF In four years (t = 4) Transaction CF Total Total Total ill. Now assume that one of your clients asks you to fix today the interest rate on a two- year $1,000 loan that she will take in exactly three years. How could you accomplish this request? Clearly state the positions that you need to take in each bond and the cash flows derived from this strategy at every relevant point in time. Include a table like the one below with your results. What rate (expressed as an EAR) will your client pay on her loan? (Hint: assume that you can trade fractions of any bond). [8 marks] Today (t = 0) Transaction CF In three years (t = 3) Transaction CF In five years (t = 5) Transaction CF Total Total Total iv. Is the interest rate on the loan of part (ill) equal to the forward rate for that period? Why? [2 marks]