A zombie virus has taken over in the United States. The CDC utilizes an elementary differential equation to predict the number of infected individuals in the population at any time if we make certain assumptions. Let us assume that all individuals in the US have an equally likely chance of becoming infected and once infected they instantly become a zombie and remain in that state. There is no known cure at this point. Let x(t) denote the number of susceptible individuals at time t and y(t) denotes the infected which in turn are zombies. It is completely reasonable to assume that the rate of change of the infected (zombies) is proportional to the number of zombies and the number of un-infected. i.e.:

(1)

where k is a constant. One way to see this is that when the number of zombies is small, then the rate of change is small as well. However, when the overall population is infected, i.e. x(t) small, then the rate of change of the zombies is small since there are fewer people left to infect. Furthermore, we can make the assumption that:

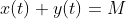where M is the total population. Now, equation (1) can be reduced to an ODE in y(t):

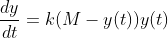(2)

In our earlier assumption, we assumed that the zombies were left in the population and allowed to infect others. A more realistic assumption would be to introduce a third variable z(t) to represent the number of zombies that are removed from the infected population at time t by either isolation or death. For example, the Walking Dead TV show uses the term mercy when exterminating zombies. Thus, these zombies cannot infect the remaining un-infected population. Nonetheless, this makes the problem even more challenging but it can be shown that an approximate solution can be given by the following:

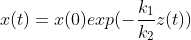(3)

(4)

where k1 is the infective rate and k2 is the removal rate. Here, z(t) is determined from:

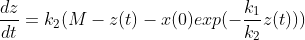(5)

There is currently no known exact solution to (5) so a numerical procedure must be applied to obtain a solution.

Find an approximation to z(30), y(30), and x(30), assuming that M = 100,000, x(0) = 99,000, k₁ =210^-6, and k₂ =10^-4.

What are the results when t = 720 days? Will the human population survive? This will help the CDC to decide on an approach to tackle this infection. Keep in mind, this computation is of the utmost importance for the survival of the human race!!!