1.  Explain why AC is the perpendicular bisector of BD.

 

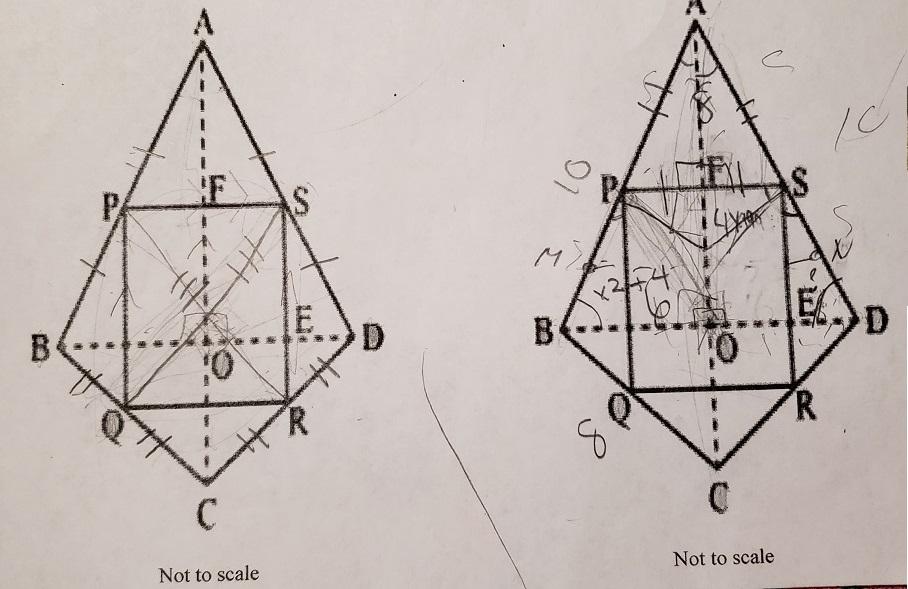
AD; BC = DC; PR = QS,; P, Q, R, and S are the midpoints of AB, BC, DC, and AD respectively, Questions 2-5: Statements in a proof are provided. Write the reason that best justifies each statement. 1) Explain why AC is the perpendicular bisector of BD. Statements Reasons AB = AD; BC = DC; PR s QS; P, Q, R, and S are the midpoints of AB, BC, DC, and AD respectively. Given 2) PQ || AC; SR || AC: PS || BD; QR | BD 2 lA aplane, 2 lines t to th suo ime. 3) PQ |I| SR; PS I| QR 3) Transative Property 4) PQRS is a parallelogram. 4) Def. of paralelogram 5) PQRS is a rectangle. The diagonals of a vectangi 5) A For the Questions 6-8, let AB = 10, BC = 8, B0 = 6, and AO = 8 6) Find the length of PS. 7) M and N are the midpoints of PB and SD respectively. Find MN. 4 8) *Let MLPBD = x2 + 4 and mzPSD = 4x + 99. If x > 0, find mzSDB. For questions 9-12, consider quadrilateral ASOP. - Note that it can be proven that AAFP = AAFS by the hypotenuse-leg theorem for triangle congruence. - Since corresponding parts of congruent triangles are congruent, PF = FS. 9) Explain why AF = OF. 10) Why is ASOP a parallelogram? 11) Why is ASOP a rhombus? 2) *Let mLSOP = 74, mLPAF = 2j +k, and mzSFO = 5j + k. Solve for the values of j and k. Questions 8 & 12, the expressions represent the measures of the stated angles to the nearest degree.