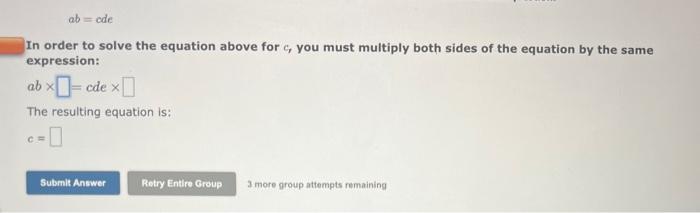
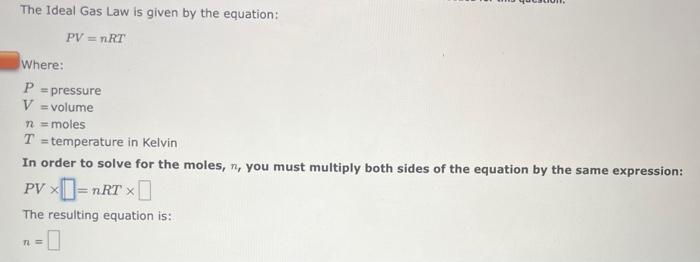
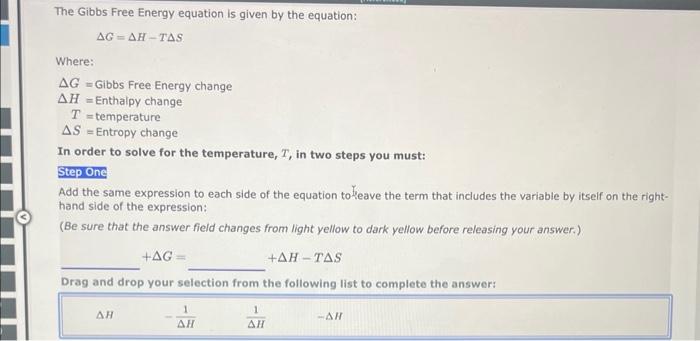
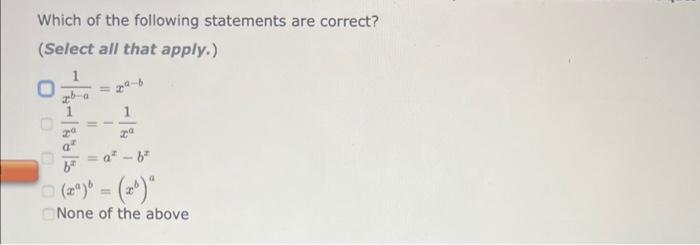
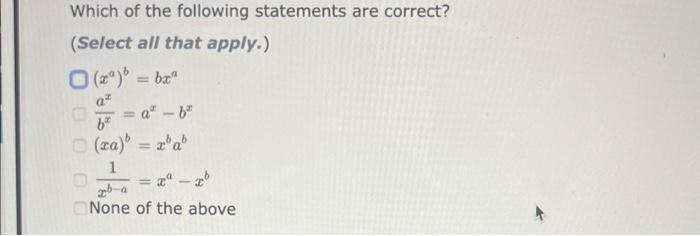
a=bcd In order to solve the equation above for b, you must multiply both sides of the equation by the same expression: a=bcd The resulting equation is: b= ab=ade In order to solve the equation above for c, you must multiply both sides of the equation by the same expression: ab=cde The resulting equation is: c= The Ideal Gas Law is given by the equation: PV=nRT Where: P=pressureV=volumen=molesT=temperatureinKelvin In order to solve for the moles, n, you must multiply both sides of the equation by the same expression: PV=nRT The resulting equation is: n= Two-Step Algebra a=bcd In order to solve the equation above for c, you must: Step One Add the same expression to each side of the equation to leave the term that includes the varlable by itself on the righthand side of the expression: +a=+bcd Two-Step Algebra a=bc+d In order to solve the equation above for c, you must: Step One Add the same expression to each side of the equation to leave the term that includes the variable by itself on the righthand side of the expression: +a=bc+d The Gibbs Free Energy equation is given by the equation: G=HTS Where: G= Gibbs Free Energy change H= Enthalpy change T= temperature S= Entropy change In order to solve for the temperature, T, in two steps you must: Step One Add the same expression to each side of the equation to Seave the term that includes the variable by itself on the righthand side of the expression: (Be sure that the answer field changes from light yellow to dark yellow before releasing your answer.) +G=+HTS Drag and drop your selection from the following list to complete the answer: HH1H1H Which of the following statements are correct? (Select all that apply.) xba1=xabxa1=xa1bxax=axbx(xa)b=(xb)a None of the above Which of the following statements are correct? (Select all that apply.) (xa)b=bxabxax=axbx(xa)b=xbabxba1=xaxb None of the above Use the References to access important values if needed for this question. The Kb of a solution can be determined from the pKb using the equation: Kb=10pKb Where: Kb=basedissociationconstant Use the rules for logarithms and exponents to solve for pKb in terms of Kb. NOTE: Capitalization counts. The Ka of a solution can be determined from the pKn using the equation: Ka=10pKs Where: Ka=aciddissociationconstant Use the rules for logarithms and exponents to solve for pKa in terms of Ka. NOTE: Capitalization counts