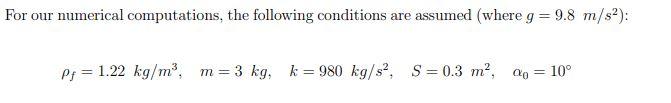
By analytical methods such a study is difficult and, in some cases, it is impossible if a high degree of accuracy is required. L cos(Aa), Aa Aa z=0 k Figure 1: Vertical motion of a wing in a wind tunnel. Figure 1 above shows schematically a wing installed in a wind tunnel. The weight of the wing, mg, is supported by a spring of spring constant k, which is equivalent to the stiffness of a wing on an airplane. The cross section of the wing is a symmetric airfoil. In the absence of wind, the airfoil makes an angle ao with the horizontal and its center of mass under a state of equilibrium is at a height z = 0. Assume that the wing is so installed that it can move only vertically. The displacement of the center of mass is 2, considered positive when going upward. The wind tunnel supplied a uniform horizontal wind speed u at the test section. When the wing moves upward at a speed v, the surrounding air moves downward relative to the wing at the same speed. Angle of Attack, Lift, & Lift Coefficient To the oncoming air flow, the angle of attack of the wing is a = a0 - . = C0 - tan (1) The lift of the wing, in the direction normal to the flow, has the expression L = P; (u? + v?) Sa (2) where p; is air density, S the projected wing area, and c the lift coefficient of the wing. According to the thin-airfoil theory for a wing of large aspect ratio, the lift coefficient is a linear function of the angle of attack, which has the following form for a symmetric airfoil: q = 2na (3) The theory agrees with experiment if a is within a certain limit. Beyond the limit the wing no longer behaves like a thin body, and the flow separates from the surface. The sudden decrease of lift associated with this phenomenon causes the wing to stall. For simplicity, let us assume that (3) holds for the wing if -18 < a < +18 and that beyond this range that the lift is zero. Equations of Motion The equations of motion for the center of mass are dz = v dt dv (4) -kz + L cos (Aa) m- dt Upon substitution of the value cos (Aa) (5) u? + v and (2) into (4) gives: dv m = -kz + apfSuvu + v? (6) dt This problem contains several parameters, and each of them may vary. Instead of solving equations in the present form for each set of parameters, it is usually more advantageous to solve them in a nondimensionalized form. In this way we only need to vary the values of a reduced number of dimensionless parameters so that a class of problems can be solved through a single computation. Nondimensionalized Equations The procedure in nondimensionalizing the governing equations is first to find the basic refer- ence quantities for the problem. In the present case of a spring supported wing, we may use the period of free oscillation of the system, 27 /m/k, as the reference time; the deformation of the spring due to the weight of wing, mg/k, as the reference length; and the ratio of the two as the reference velocity. Based on these reference quantities, the following dimensionless variables are defined: k 27 k Z = 2- mg (7) 27 7 = u- k k V = v m After being expressed in terms of these dimensionless variables, the dimensionless form of the equations of motion become dz dt (8) = - (27)z + Bcva+7? with the dimensionless parameter Spfg 2k Thus, the six parameters p7, g, m, S, k, and u are reduced to only two dimensionless groups, 3 and . Each set of values of and represents a large number of combinations of the dimensionless parameters. For our numerical computations, the following conditions are assumed (where g = 9.8 m/s): Ps = 1.22 kg/m, m 3 kg, k = 980 kg/s2, S= 0.3 m2, 10 Suppose that superimposed on the uniform flow that there is a fluctuating horizontal velocity component so that the total velocity can be expressed in dimensionless form 7 (1+ a sin wi) where the fluctuation has an amplitude a, and its frequency is w times the natural frequency of the wing. Modify (8) to handle this fluctuating horizontal velocity