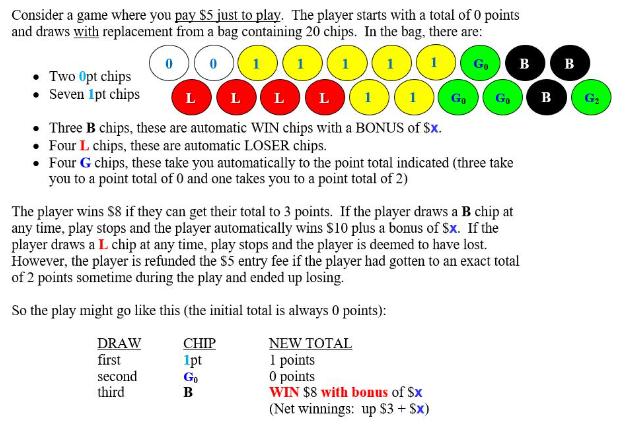
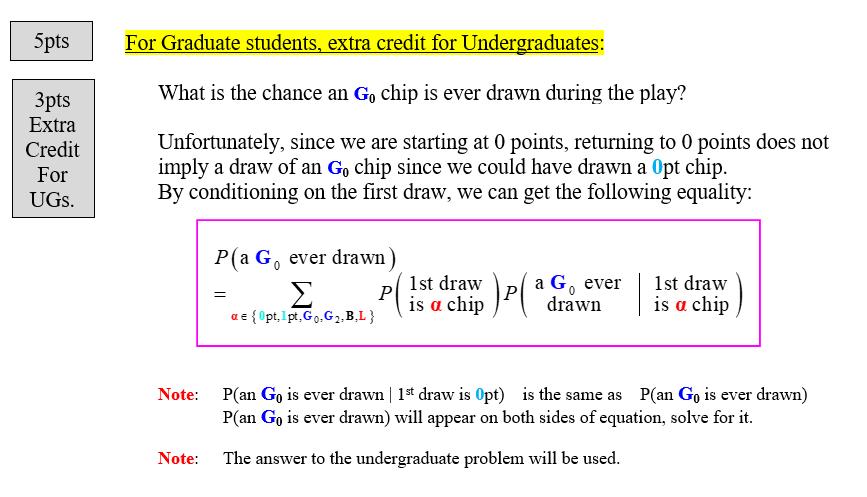
Consider a game where you pay $5 just to play. The player starts with a total of 0 points and draws with replacement from a bag containing 20 chips. In the bag, there are: 000000 111111 Two Opt chips Seven 1pt chips 85 Three B chips, these are automatic WIN chips with a BONUS of $x. Four L chips, these are automatic LOSER chips. Four G chips, these take you automatically to the point total indicated (three take you to a point total of 0 and one takes you to a point total of 2) Go B G B The player wins $8 if they can get their total to 3 points. If the player draws a B chip at any time, play stops and the player automatically wins $10 plus a bonus of Sx. If the player draws a L chip at any time, play stops and the player is deemed to have lost. However, the player is refunded the $5 entry fee if the player had gotten to an exact total of 2 points sometime during the play and ended up losing. So the play might go like this (the initial total is always 0 points): DRAW CHIP NEW TOTAL first 1pt 1 points second Go 0 points third B WIN $8 with bonus of $x (Net winnings: up $3 + $x) B Or the play might go like this (the initial total is 0 points): DRAW CHIP NEW TOTAL first second third fourth G Go 1pt L first second Or the play might go like this (the initial total is 0 points): DRAW CHIP NEW TOTAL first second Opts L 2 points 0 points 1 point REFUND, since we attained the 2 points mark (Net winnings: $0) G 1pt Or the play might go like this (the initial total is 0 points): DRAW CHIP NEW TOTAL 0 points LOSE COMPLETELY (Net winnings: - $5) 2 points WIN $8, no bonus (Net winnings: up $3) 4pts Our main goal will be to determine the chance of "losing completely", resulting in a net gain of -$5 a "refund", resulting in a net gain of $0 "winning, no bonus", resulting in a net win of $3 "winning, with bonus", resulting in a net win of $3 + $x Note: these 4 chances must sum to 100%. We will monitor the total points as Markov Chain with states: LOSE, 0 points, 1 point, 2 points, WIN. a) Fill in the components of the basic transition probability matrix: 012 Win P = Lose 0 1 2 Win Lose 4pts b) Find the S matrix. Determine: S = 0 2 0 1 2 row sum= row sum= row sum= Average number of draws needed to complete the game: Assuming the first draw was the G chip, on average, how many total draws - including the draw of the G chip - are required to complete the game? 6pts c) Insert a relay state called "Rose" which is passed though right before one goes to the state "LOSE". Find the corresponding S matrix. One should see that the probability of drawing the L chip is 1996/4011. Note: this is the sum of the chances of "losing completely" and "refund". S = R. lose 0 1 2 lose 1 1996 4011 0 0 1 0 2 0 Assume the first draw was 1pt chip. Conditional on obtaining a point total of 1, what is the reduced chance that we ever draw an L chip? 4pts d) Determine the following 4 probabilities: P(losing completely) P(refund) = P(winning, no bonus) P(winning, w/ bonus) Note: = = with a net gain of -$5 with a net gain of $0 with a net gain of $3 with a net gain of $3 + $x P(refund)=P(get to a total of 2 points AND draw the L chip) = P(get to a total of 2 points) * P(draw the L chip | total of 2 points) P(draw the L chip) = P(losing completely) + P(refund) = 1996/4011 P(draw the B chip) = 4 * P(draw the L chip). All 4 probabilities add to 1. This is logical since the number of B chips is 75% of the number of L chips. 4pts 5pts e) What should be the value of the bonus $x so that this is a fair game? BONUS $x = $ Note: fair games have expected net gains of 0. f) Using the S matrix found in part (b), find For Undergraduate students only: Given that our first draw is a 1pt chip, what is the chance that we ever draw an Go chip anytime during the play of the game? Hint: given we are currently in state 1 point, the only way to get back to state 0 points is to draw a Go chip. So: P(ever draw Go | X = 1) is equivalent to P(return to state 0 | X = 1) 5pts 3pts Extra Credit For UGS. For Graduate students, extra credit for Undergraduates: What is the chance an Go chip is ever drawn during the play? Unfortunately, since we are starting at 0 points, returning to 0 points does not imply a draw of an Go chip since we could have drawn a opt chip. By conditioning on the first draw, we can get the following equality: P(a G, ever drawn) ae {Opt, Ipt, Go, G.B.L} Note: = P 1st draw is a chip P a Go ever drawn 1st draw is a chip Note: P(an Go is ever drawn | 1st draw is Opt) is the same as P(an Go is ever drawn) P(an Go is ever drawn) will appear on both sides of equation, solve for it. The answer to the undergraduate problem will be used.