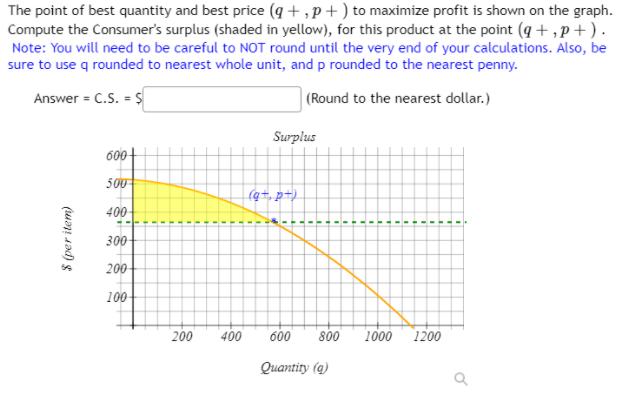
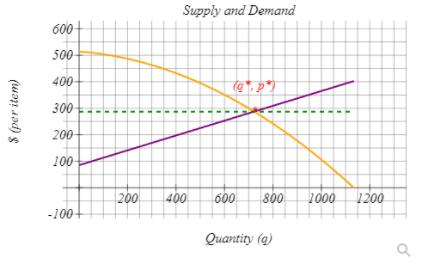
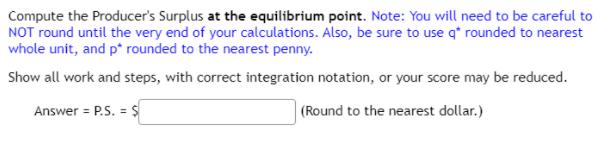
•  

The point of best quantity and best price (q+,p+) to maximize profit is shown on the graph. Compute the Consumer's surplus (shaded in yellow), for this product at the point (q+,p+). Note: You will need to be careful to NOT round until the very end of your calculations. Also, be sure to use q rounded to nearest whole unit, and p rounded to the nearest penny. Answer = C.S. = $ (Round to the nearest dollar.) Surplus 600+ 500 400- 300 200- 100 200 400 600 800 1000 1200 Quantity (a) $ (per item) (8.4) Recall that D(q) - 0.00034g? 0.068q + 514 and S(q) = 0.28q + 85 . Find the quantity and price combination that represents the equilibrium point for your supply and demand curves. This is written as (q*.p") on the graph. Write you answer in the form (q, p) . Round your equilibrium quantity to the nearest whole unit and then use THAT value in the SUPPLY FUNCTION to find the equilibrium price, rounded to the nearest penny. If you don't do this, you may end up with the wrong value for p*. Answer: (q*,p") = Check the reasonableness of your answer against your supply and demand curves, which look like this: Orange = Demand, Purple = Supply, Green = Equilibrium Price (drawn as a line) %3D %3D Supply and Demand 600 500 400 300 200 100 200 400 600 800 1000 1200 -100 Quantity (a) $ (per item) %3D Let's assume that we are forced to set our price at the equilibrium price due to competition. Use your values for the equilibrium quantity (q*) and price (p*) to compute the Consumer's Surplus at the equilibrium point. Note: You will need to be careful to NOT round until the very end of your calculations. Also, be sure to use q* rounded to nearest whole unit, and p* rounded to the nearest penny. Show all work and steps, with correct integration notation, or your score may be reduced. Answer C.S. S |(Round to the nearest dollar.) Compute the Producer's Surplus at the equilibrium point. Note: You will need to be careful to NOT round until the very end of your calculations. Also, be sure to use q* rounded to nearest whole unit, and p* rounded to the nearest penny. Show all work and steps, with correct integration notation, or your score may be reduced. Answer = P.S. = $ (Round to the nearest dollar.) Cost function: C(q)=104.2q+11700 Demand function: D(g)=-0.00034q^2-0.068q+514 Supply function: S(q)=0.28q+85