a.)Derive an expression of the formula for pricing a cashflow presented (labelled, In General),

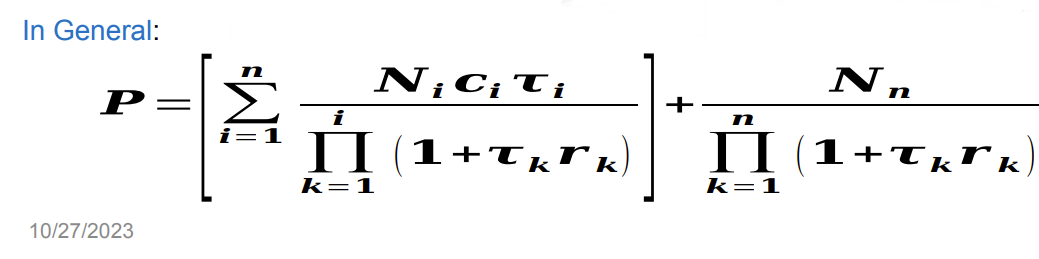
assuming constant Notional (N), constant accrual periods (), and the coupon rate (c) to be Overnight Libor rate and the discounting rate (r) to be Fed Fund Rate. Next express the Overnight Libor (coupon rate) as a Fed Fund Rate plus a basis. What will be the value of the basis if the value of the cashflow is at Par (same as Notional (N))? Can there be a non-zero (non-constant) basis for which the cashflow remains at par? Can you think of constructing a swap around the cashflow which can be used to hedge the basis risk? Express the present value of the two legs of the swap using formulas.

b)Consider the case where a Hedge Fund (HF) gets a Loan from a Prime-Brokerage Firm (PB) of Notional Amount N (= 200MM USD) for maturity T (= 5years) at an interest rate of r0 (= 10% per annum), to be paid out every quarter-end, with the full Notional paid at maturity. The loan is not amortized (constant Notional) and cannot be prepaid. PB treats this Loan to be at par (Present Value = N) for its internal books and records, assuming the risk-free interest rate to be d (= 2% per annum), a constant through the maturity of the loan. HF requests PB to consider reducing the required interest-rate on the Loan-payments, for which HF is willing to post a collateral amount of C (= 50MM USD). Assuming that the credit spread diminishes linearly with the amount of collateral Fall 2023, FRE 6901 3 | Page posted and vanishing at full-collateralization, show that the revised interest-rate, that PB will be willing to offer HF, keeping the loan at par will be (derive step-by-step stating all assumptions):

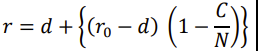
First derive the above formula, using just the variables (without using any values)

After you have successfully derived the formula, use the above values of the variables in the formula to calculate the value of the revised interest rate.

Additionally, also calculate the net savings (without discounting effects) made by HF in loan-payments through the maturity by posting the collateral.

Need complete solution for this .

In General: P=[i=1nk=1i(1+krk)NiCii]+k=1n(1+krk)Nn 10/27/2023 r=d+{(r0d)(1NC)}