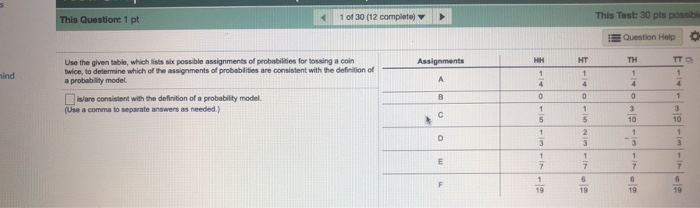
a)Describe the statistical significance of each of the independent variables included in the Mrs. Smyth's demand equation. Interpret the coefficient of determination and F statistic for the multiplicative model.

b)Compare the statistical properties of your multiplicative model with the linear model. Which fits the data better? Explain why.

c)In the multiplicative model perform a statistical test to determine whether demand is elastic, your competitor's product is a substitute, and if pies are a normal good at the 95 percent confidence level.

d)What is your estimate of the price elasticity of demand, advertising elasticity of demand, income elasticity of demand, and cross price elasticity of demand in the multiplicative model? Compare these elasticity estimates with the corresponding elasticities in the linear model when calculated at mean values for each variable.

e)Using the linear model, what is the expected value of next quarter's unit sales in the Los Angeles-Long Beach-Santa Ana, CA market? Use the value of each independent variable for the last period in the MN market for this forecast. Derive the 95 percent confidence interval for next quarter's actual sales in the Minneapolis- St. Paul market.

Question 5: A manufacturer produces bolts that are specified to be between 1.19 and 1.21 inches in diameter. If its production process results in a bolt's diameter being normally distributed with mean 1.20 inches and standard deviation 0.004, what proportion of bolts will not meet specifications?Question 4: The time until failure of a certain type of fan used in a diesel engine follows an exponential distribution with mean 25,000 hours. a) Identify the value of 2. b) What is the probability that a randomly selected fan will last at least 10,000 hours? c) What is the probability that two randomly selected fans of this type will last at least 10,000 hours? d) What is the probability that a randomly selected fan will last between 20,000 and 30,000 hours? e) What is the probability that a randomly selected fan will last at least 50,000 hours given it has lasted 40.000 hours?1. (a) Explain what is meant by the transition probability matrix of a homogeneous Markov chain. [5 marks] (b) Explain what is meant by the stationary distribution of a Markov chain? [5 marks] (c) A Markov chain has transition probability matrix, A, with entries Ouj; and stationary distribution . Write down an expression for the entries of the reverse Markov chain. [5 marks (d) Consider the following transition probability matrix of a homogo- neous Markov chain, with three states i,j and k (the TPM is in that order). If the stationary vector of the chain is (1/9, 2/9, 2/3), determine whether the Markov chain is reversible. 1 /0.2 0.2 0.6 0.1 0.6 0.3 4 \\0.1 0.1 0.8 [5 marks] (e) Let X1, X2, Xa be a sequence of random variables resulting from the above Markov chain. If X1 = i and Xs = j what is the probability that X2 = k? [5 marks]This Question: 1 pt 1 of 30 (12 complete) + This Test: 30 pts possibl Question Help Use the given table, which lists six possible assignments of probabilities for tossing a coin Assignments HH HT TH TT twice, to determine which of the assignments of probabilities are consistent with the definition of probability model. A Ware consistent with the definition of a probability model. 1 (Uve a comma to separate answers as needed.) 10 10 D - 4- F 19We will explore the continuous uniform distribution in this question. Part I) Say that you observe five random variables from the continuous uniform distribution on 0 to 0. This means that f(= ) = 1 if O