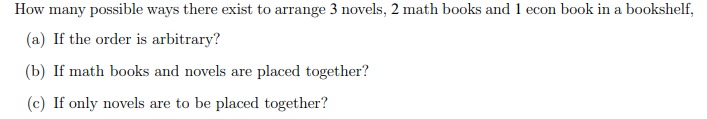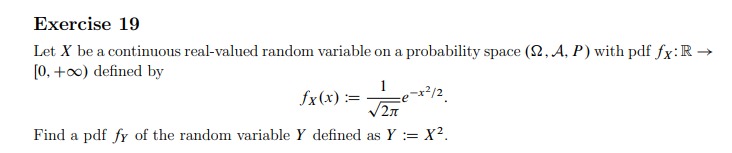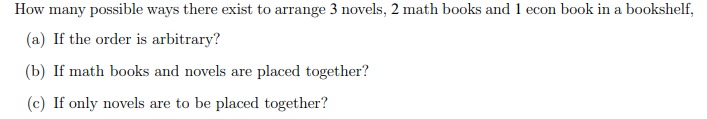






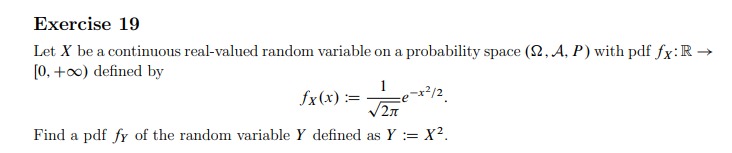
Advanced Econ
How many possible ways there exist to arrange 3 novels, 2 math books and 1 econ book in a bookshelf, (a) If the order is arbitrary? (b) If math books and novels are placed together? (c) If only novels are to be placed together?A fair die is rolled for three times. (a) What is the probability that no even number occurs? (b) What is the probability to obtain an increasing sequence of numbers? (c) What is the probability to obtain a strictly increasing sequence of numbers? Briefly explain your reasoning.Solve the following problems. (a) Let X be a metric space, and denote with Ox and Cy the class of all open and closed subsets of X, respectively. Is either Ox or Cx a field on X? A o-field? How about Ox UCx? Justify your answers. Note. A positive answer needs a proof, while for negative answers a counterexample suffices. (b) Let (2, A) be a measurable space and pick any @ 6 2. Consider the function 8: A - (0, 1} defined by 80(A) = if we A else Show that 8, is a probability measure on (2, A). It is called the Dirac (probability) measure on (2, A). (c) (Borel-Cantelli Lemma) Let ($2, A. P) be a probability space and { A,,) ~ a sequence of events in A such that _ P(A,) , Am. Show that OO P n Bn = 0. 1=1Let P be a probability measure on (R. B(R)), where B(R) denotes the Borel o-field on R, and define A:= (AE B(R) : P(A) = (0, 1 } }. Show that A is a o-field on R.Let E] be a nonempty set and I a nonempty index set. Moreover, suppose that A,- is a o-algebra on Q for each i E I. [a]- Show that [FL-E: .11.- is a (tralgebra on 51. {b} Let A." be a nonemptyr class of subsets of H. Show that the smallest nalgebra on R generated by A\" is welldened [i.e., show that it exists and that it is unique}. [12} Give an example to show that Ute: A.- need not be an algebra even if I is a nite set. Try to some up with an example which is as simple as possible. {d} Now suppose that I = H and that .31.- E A.\" for lashi E N. Show that UieNvd'i is an algebra on E. but it need not be a oalgebra. [Na-ts. A much stronger statement is actually true. Namely: if A; C Ai+1 for each i E N, where the inclusion is now proper, then Um\" A.- ean never be a cralgebra. You can tr}.r to establish this result.| but it is not too trivial.] Solve the following problems. (a) Let P be a probability measure on (R. B(R)) and define the function F: R - [0, 1] as F(b) := P((-oo, b]) for all be R. Show that: (i) P((a,b]) = F(b) - F(a) for all a, b e R with a